Bilder in der Quantenmechanik

Julian Schultheiss
Methoden der Beschreibung der
Zeitentwicklung in der Quantenmechanik. Im Schrödinger-Bild wird die
Zeitentwicklung durch zeitabhängige Zustandsvektoren ![]() beschrieben; die grundlegende
Bewegungsgleichung ist die Schrödinger-Gleichung
beschrieben; die grundlegende
Bewegungsgleichung ist die Schrödinger-Gleichung
![]() .
.
(H: Hamilton-Operator). Das Schrödinger-Bild steht in engem Zusammenhang mit der Schrödingerschen Wellenmechanik.
Im Heisenberg-Bild hingegen werden die Zustände als zeitunabhängig angenommen, während die Operatoren zeitlich veränderlich sind; entsprechend ist die Bewegungsgleichung, die Heisenberg-Gleichung, eine Operatorgleichung für einen Operator AH:
![]() .
.
Die eckigen Klammern bezeichnen den üblichen Kommutator. Das Heisenberg-Bild hat seine Wurzeln in der Heisenbergschen Matrizenmechanik.
Im von Dirac eingeführten Wechselwirkungsbild
(Dirac-Darstellung) werden sowohl der Zustand als auch die Operatoren als
zeitabhängig betrachtet; dies ist sinnvoll, wenn der Hamilton-Operator ![]() in einen zeitunabhängigen Anteil H0 und einen
zeitabhängigen Anteil
in einen zeitunabhängigen Anteil H0 und einen
zeitabhängigen Anteil ![]() zerfällt. Die Bewegungsgleichungen lauten
dann:
zerfällt. Die Bewegungsgleichungen lauten
dann:
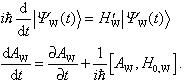
Die beschriebenen Darstellungsarten sind mathematisch
äquivalent; der Übergang zwischen dem Heisenberg- und dem Schrödinger-Bild wird
durch entsprechende Anwendungen des unitären Zeitentwicklungsoperators ![]() bewirkt:
bewirkt:
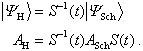
Der Übergang zum Wechselwirkungsbild vollzieht sich mittels
des Operators ![]() gemäss:
gemäss:
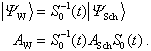
Techniklexikon.net
Das freie Technik-Lexikon. Fundierte Informationen zu allen Fachgebieten der Ingenieurwissenschaften, für Wissenschaftler, Studenten, Praktiker & alle Interessierten. Professionell dargeboten und kostenlos zugängig.
Techniklexikon
Modernes Studium der Physik sollte allen zugängig gemacht werden.