Zweikörperproblem

Irene Kramer-Schwenk
Klassische
Mechanik, Problem der Bewegung zweier Massenpunkte m1 und m2
unter dem alleinigen Einfluss ihrer gegenseitigen Wechselwirkung. Man legt
zweckmässigerweise den Ursprung des Koordinatensystems in den Schwerpunkt und
separiert die Relativbewegung von der Schwerpunktsbewegung. Das Problem
reduziert sich damit auf die Bewegung eines einzigen, fiktiven Körpers mit der
reduzierten Masse des Systems, mit dem Ortsvektor r
= r1 - r2 der Relativbewegung der
Massenpunkte (siehe Abb.) und unter Einfluss der auf den Körper 1 wirkenden
Kraft ![]() . Für
Kräfte, die nur vom gegenseitigen Abstand der Körper abhängen, vereinfacht sich
die Bewegung auf die eines Teilchens im kugelsymmetrischen Zentralfeld, in dem
Drehimpulserhaltungssatz und Energiesatz gelten. Ein Beispiel ist das
Zweikörperproblem der Himmelsmechanik, die auch Kepler-Problem genannte
Bestimmung der Planetenbewegung, dessen Lösung erstmals in guter Näherung durch
die Keplerschen Gesetze aus Beobachtungsmaterial bestimmt wurde. Ähnlich kann
die Coulomb-Kraft, d.h. die elektrostatische Anziehung zweier Ladungen,
behandelt werden. Da diese Kraft die gleiche räumliche Abhängigkeit wie die
Newtonsche Massenanziehung hat, sind die dabei auftretenden Bahnkurven
ebenfalls Kegelschnitte; man spricht daher bei der Bestimmung der Bewegungen
des Elektrons im Wasserstoffatom vom Kepler-Problem der Atomphysik, wobei
allerdings zusätzlich die Quanteneigenschaften dieser Bewegung zu
berücksichtigen sind. In beiden Fällen entspricht die zeitliche Änderung des
Relativvektors r einer Zentralbewegung.
. Für
Kräfte, die nur vom gegenseitigen Abstand der Körper abhängen, vereinfacht sich
die Bewegung auf die eines Teilchens im kugelsymmetrischen Zentralfeld, in dem
Drehimpulserhaltungssatz und Energiesatz gelten. Ein Beispiel ist das
Zweikörperproblem der Himmelsmechanik, die auch Kepler-Problem genannte
Bestimmung der Planetenbewegung, dessen Lösung erstmals in guter Näherung durch
die Keplerschen Gesetze aus Beobachtungsmaterial bestimmt wurde. Ähnlich kann
die Coulomb-Kraft, d.h. die elektrostatische Anziehung zweier Ladungen,
behandelt werden. Da diese Kraft die gleiche räumliche Abhängigkeit wie die
Newtonsche Massenanziehung hat, sind die dabei auftretenden Bahnkurven
ebenfalls Kegelschnitte; man spricht daher bei der Bestimmung der Bewegungen
des Elektrons im Wasserstoffatom vom Kepler-Problem der Atomphysik, wobei
allerdings zusätzlich die Quanteneigenschaften dieser Bewegung zu
berücksichtigen sind. In beiden Fällen entspricht die zeitliche Änderung des
Relativvektors r einer Zentralbewegung.
Das Zweikörperproblem der Allgemeinen Relativitätstheorie ist nicht in geschlossener Form lösbar. In erster Näherung ergibt sich die Kepler-Bewegung der Newtonschen Mechanik, in zweiter Näherung folgt eine Drehung der grossen Halbachse der Ellipsenbahnen der Himmelskörper (Periheldrehung).
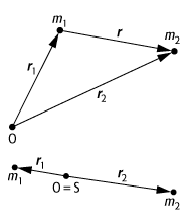
Zweikörperproblem: Die Schwerpunktsbewegung lässt sich von der Relativbewegung (oben) separieren, wenn man den Ursprung O des Koordinatensystems in den Schwerpunkt S legt (unten).
Techniklexikon.net
Das freie Technik-Lexikon. Fundierte Informationen zu allen Fachgebieten der Ingenieurwissenschaften, für Wissenschaftler, Studenten, Praktiker & alle Interessierten. Professionell dargeboten und kostenlos zugängig.
Techniklexikon
Modernes Studium der Physik sollte allen zugängig gemacht werden.