Techniklexikon

Riemannscher Zusammenhang

Relativitätstheorie und Gravitation, affiner Zusammenhang, Konnexion, kann in einer Riemannschen Geometrie entweder als Ableitungsoperator  eingeführt werden, welcher angewandt auf die Metrik zu

führt, oder mittels der Geodätengleichung (Geodäte). Dabei sind die Komponenten des Riemannschen Zusammenhangs gegeben durch:

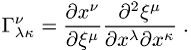
Diese lassen sich auch durch die Metrik ausdrücken: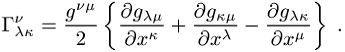

Die Komponenten des affinen Zusammenhangs  werden auch als Christoffel-Symbole (Christoffel-Konnexion) bezeichnet. Der affine Zusammenhang ist kein Tensor; er verschwindet stets in lokalen Inertialkoordinaten, im allgemeinen aber nicht in beliebigen Koordinaten. In globalen Inertialkoordinaten verschwindet der affine Zusammenhang überall, und die Geodätengleichung geht in die Bewegungsgleichung für ein freies Teilchen über.