Techniklexikon

Poisson-Klammern

Klassische Mechanik, ein in der Analytischen Mechanik gebräuchlicher Operator, der auf Funktionen der kanonischen Impulse und Koordinaten  wirkt und eng mit den Lagrange-Klammern verwandt ist. Die Poisson-Klammern sind definiert als

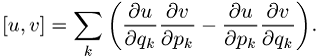
Für alle kanonischen Variablen p_k, q_k  gelten die fundamentalen Posisson-Klammern

, unabhängig vom Satz der gewählten kanonischen Variablen. Für eine beliebige Funktion F(q_i,p_i) gilt

Wird als Funktion F die Hamilton-Funktion H gewählt, so lassen sich die Hamiltonschen Bewegungsgleichungen elegant schreiben als . Man kann zeigen, dass eine Funktion, deren Poisson-Klammer mit der Hamilton-Funktion identisch verschwindet, eine Konstante der Bewegung des Problems ist. Weiterhin ist die Poisson-Klammer zweier Konstanten der Bewegung eine ebensolche. So lassen sich ganze Serien von Konstanten der Bewegung konstruieren, von denen sich jedoch zahlreiche als trivial entpuppen. Die tiefere Bedeutung der Poisson-Klammern liegt darin, dass sie einen der Berührungspunkte der Hamiltonschen Mechanik mit der Quantenmechanik darstellen. Die Poisson-Klammer entspricht dem mit 2p / ih multiplizierten Kommutator zweier Grössen.