Molekülorbitaltheorie

Chemie, Physikalische Chemie, MO-Methode, molecular orbital method, ein quantenmechanisches Näherungsverfahren zur Berechnung der Elektronenstruktur und der Energie von Molekülen, das im wesentlichen von Hund, Mulliken, Lennard-Jones und Hückel (1927-29) entwickelt wurde. Dabei betrachtet man analog dem Zentralfeldmodell der Atome ein Elektron, das sich in einem effektiven Potential der Kerne und der übrigen Elektronen bewegt. Die daraus resultierenden Einelektronenzustände des Moleküls bezeichnet man als Molekülorbitale (Abk. MO) mit der Wellenfunktion F. Sie erstrecken sich über das gesamte Molekül und sind durch eine Orbitalenergie gekennzeichnet. Die Besetzung der energetisch niedrigsten Molekülorbitale unter Beachtung des Pauli-Prinzips führt zur Elektronenkonfiguration der Moleküle im Grundzustand. Die mathematische Darstellung von F als Linearkombination von Atomorbitalen mit Wellenfunktionen y_i stellt einen geeigneten Näherungsansatz dar (MO-LCAO-Ansatz, Abk. von molecular orbitals - linear combination of atomic orbitals): . Beim Variationsverfahren werden die Koeffizienten c_i so gewählt, dass die Energie des Gesamtsystems einen Minimalwert annimmt.

Das Prinzip der Molekülorbitalmethode lässt sich am einfachsten für homonukleare zweiatomige Moleküle, z.B. für das -Molekül, demonstrieren. Die Kombination der 1s-Orbitale der beiden Wasserstoffatome A und B führt zu zwei Molekülorbitalen . Die entsprechenden Orbitalenergien E₊ und E_- weisen gegenüber der Energie der Atomorbitale eine niedrigere bzw. höhere Energie auf. Daher bezeichnet man den Zustand F₊ als bindendes und F_- als lockerndes (antibindendes) Molekülorbital. Im Grundzustand des Wasserstoffmoleküls besetzen beide Elektronen das bindende Molekülorbital. Damit kann die chemische Bindung im Wasserstoffmolekül erklärt werden.

Analog zu den 1s-Orbitalen können auch andere Atomorbitale zu Molekülorbitalen kombinieren. Auf Grund der durch die Winkelteile bestimmten Symmetrie und Richtungsabhängigkeit der Atomorbitale unterscheidet man verschiedene Überlappungsmöglichkeiten. Die Kombination von rotationssymmetrisch zur Bindungsachse angeordneten Orbitalen liefert s-Molekülorbitale. Sie sind durch ein Überlappungsgebiet in der Bindungsachse gekennzeichnet. Die Wechselwirkung von Atomorbitalen, die eine Antisymmetrieebene in der Bindungsachse aufweisen, führt zu p-Molekülorbitalen. Sie bilden zwei Überlappungsgebiete ausserhalb der Bindungsachse, die durch eine Knotenebene getrennt sind. Treten vier Überlappungsgebiete ausserhalb der Bindungsachse auf, die durch zwei senkrecht zueinander stehende Knotenebenen getrennt sind, so liegt ein d-Molekülorbital vor. Die so gebildeten Bindungen werden als s, p- bzw. d-Bindung bezeichnet. Die jeweils lockernden Molekülorbitale werden zusätzlich durch einen Stern markiert, z.B. s*, p*, d*. Sie weisen neben den Knotenflächen der beteiligten Atomorbitale noch eine zusätzliche Knotenfläche zwischen den Atomen senkrecht zur Kernverbindungsachse auf.

Ausgehend von den Überlappungsmöglichkeiten der Atomorbitale kann die Molekülorbitalbehandlung auf homonukleare zweiatomige Moleküle von Elementen der 2. Periode (Li₂, B₂, C₂, N₂, O₂, F₂) ausgedehnt werden. Der MO-LCAO-Ansatz kann auch auf kompliziertere Moleküle angewendet werden, wobei der Rechenaufwand mit steigender Anzahl von Atomorbitalen stark zunimmt.

Mit einer Kombination aus Elektronenstrahl- und Röntgenbeugung konnten J.-M. Zuo, J.C.H. Spence und Kollegen die Molekülorbitale in Kupfer(I)oxid sichtbar machen (siehe Abb.) und nachweisen, dass dabei neben ionischen Bindungen auch kovalente Bindungen (chemische Bindung) sowie - überraschenderweise - Bindungen zwischen den Metallatomen auftreten.

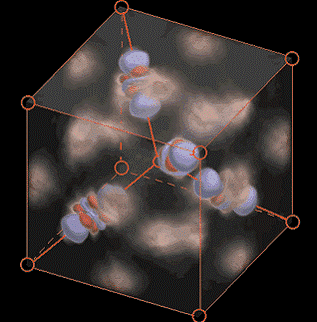
Molekülorbitaltheorie: In Messungen an Cuprit (CU₂O) gefundene kompliziert geformte Orbitale, die aus der Hybridisierung von einem s- und zwei d_z-Orbitalen hervorgegangen sind. Ihr Aussehen entspricht genau den theoretischen Berechnungen: eine Hantel mit einem Ring und zwei weiteren Ringen (J.M. Zuo, M. Kim, M. O'Keeffe und J.C.H. Spence: Nature 401, 49 (1999)).