Techniklexikon

Liouville-Gleichung

lineare partielle Differentialgleichung, die die Änderungsrate der Phasenraumdichte  an einem festen Punkt im Phasenraum beschreibt:

wobei  der mit der Hamilton-Funktion gebildete Differentialoperator (Liouville-Operator)

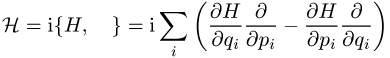
ist (: Poisson-Klammer). Daraus folgt für die zeitliche Entwicklung von r

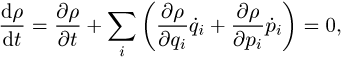
d.h. die Phasenraumdichte verhält sich wie eine volumenerhaltende inkompressible Flüssigkeit, oder anders ausgedrückt: eine Punktwolke im Phasenraum verändert im Laufe der Zeit zwar ihre absolute Lage und die relative Lage der Punkte zueinander, das einmal gegebene Volumen dieses Ensembles bleibt aber konstant (Liouvillescher Satz).

In der Quantenstatistik lautet die Liouville-Gleichung

wobei  der Dichteoperator und  der Hamilton-Operator ist.