Techniklexikon

Clebsch-Gordan-Koeffizienten

Vektorkopplungskoeffizienten, Wigner-Koeffizienten, Vektorentwicklungskoeffizienten, die die Addition quantenmechanischer Drehimpulse bei der Kopplung zweier Drehimpulseigenvektoren beschreiben. Sind  und  Drehimpulseigenvektoren der kommutierenden Drehimpulsoperatoren  und , wobei die Basis des gekoppelten Systems durch  gegeben ist (zum Beispiel in einem Zweiteilchensystem), so koppeln diese wie folgt zu Eigenvektoren  des Gesamtdrehimpulses

Die Vektorentwicklungskoeffizienten  werden als Clebsch-Gordan-Koeffizienten bezeichnet. Phasenfaktoren in der Linearkombination werden dabei so gewählt, dass die Clebsch-Gordan-Koeffizienten reell sind (Condon-Shortley-Konvention). Die Clebsch-Gordan-Koeffizienten sind nur dann von null verschieden, falls  und M = m₁ + m₂. Anstelle der Clebsch-Gordan-Koeffizienten verwendet man auch häufig die Wigner-3j-Symbole. Mit Hilfe dieser Symbole lassen sich die Symmetrieeigenschaften der Clebsch-Gordan-Koeffizienten verdeutlichen, da sie sich bei Vertauschen der Spalten oder Ersetzen von m_i durch  - m_i bzw. M durch  - M mit dem Faktor  multiplizieren.

Die Clebsch-Gordan-Koeffizienten erfüllen die Orthogonalitätsrelationen:

  .

Die Clebsch-Gordan-Koeffizienten können durch folgenden Ausdruck berechnet werden:

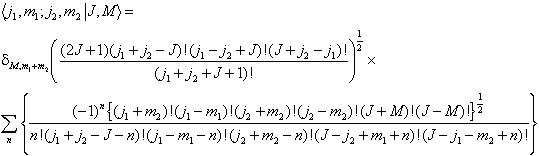
Die Summe läuft dabei über alle n, so dass die Fakultäten immer definiert, also positiv, sind. Koppelt man mehr als zwei Drehimpulseigenvektoren, so werden die dabei auftretenden Summen von Produkten der Clebsch-Gordan-Koeffizienten durch die Racah-Koeffizienten W(abcdef) ausgedrückt, wobei a, b, c, d, e, f Drehimpulsquantenzahlen sind. (Drehimpuls) [MM1]