Techniklexikon

Auslöschungsregeln

Gesetzmässigkeiten, denen das Verschwinden bestimmter Reflexe bei der Kristallstrukturanalyse unterliegt. Solche Auslöschungen lassen Rückschlüsse auf Elemente der Punktsymmetrie und auf Zusatzsymmetrieelemente (d.h. Schraubenachsen und Gleitspiegelebenen, Symmetrieelemente) des Kristalls zu. Das Zustandekommen von Auslöschungen sei am folgenden Beispiel illustriert: Ein Röntgenstrahl fällt unter dem Glanzwinkel auf die (100) Netzebenenschar eines kubischen Gitters ein, zwischen die eine weitere, gleichwertige so eingeschoben ist, dass sich ein kubisch raumzentriertes Gitter ergibt. Die an den Zwischenebenen reflektierten Wellen löschen jetzt die (100) Reflexe aus, da der Gangunterschied gerade p beträgt. Man spricht hier von einer allgemeinen oder integralen Auslöschungsregel, da sie das gesamte (reziproke) Gitter betrifft. Solche Auslöschungen treten bei basis-, raum- oder flächenzentrierten Strukturen auf.

Wenn sich die Auslöschungen über eine Ebene des reziproken Gitters (z. B. (hk0)) erstrecken, so hat man es mit zonalen Auslöschungsregeln zu tun, die auf das Vorliegen von Gleitspiegelebenen schliessen lassen.

Seriale Auslöschungsregeln gelten für Systeme, in denen Schraubenachsen vorhanden sind. Hier erstreckt sich die Auslöschung auf Reflexe, deren reziproke Gitterpunkte auf einer Geraden liegen, z.B. die Reflexe (0k0).

Die Auslöschungsregeln werden durch den Strukturfaktor F(hkl) wiedergegeben, wenn man die Terme der asymmetrischen Einheit und der symmetrieabhängigen Atomlagen aufspaltet, indem man letztere in einem je nach Raumgruppe verschiedenen Symmetriefaktor S(hkl) zusammenfasst: F(hkl) =  S(hkl). Dabei ist f_i der Atomformfaktor, N die Anzahl der Atome im Kristall und n die Anzahl der Symmetrieoperationen, die sich auf die Atomlagen anwenden lassen, d.h. N/n ist die Anzahl der Atome in der asymmetrischen Einheit. S(hkl) und F(hkl) weisen die gleichen Symmetrien auf. Ein Beispiel: Der Symmetriefaktor für ein raumzentriertes Gitter mit den Punktlagen XYZ, (X + 1/2) (Y + 1/2) (Z + 1/2) ist gegeben durch S(hkl) = 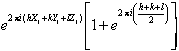. Hier werden alle Reflexe mit ungeradem h + k + l ausgelöscht.

Anhand der systematischen Auslöschungen ist man in der Lage, die möglichen Raumgruppen eines untersuchten Kristalls einzuschränken. Mit der Kombination aller Auslöschungsbedingungen lassen sich 120 Fälle, die Auslöschungseinheiten, unterscheiden. Es existieren jedoch 230 Raumgruppen. Daher lassen sich die Raumgruppen eines Kristalls mit Hilfe der systematischen Auslöschungen nicht eindeutig festlegen.

Abschliessend sei angemerkt, dass bei hinreichend intensiver Röntgenstrahlung infolge von Mehrfachstreuung im Gitter (Renninger-Effekt, Raumgitterinterferenzen) auch Reflexe erscheinen können, die nach den Auslöschungsregeln eigentlich verboten sind.