Techniklexikon

Taylor-Reihe

Mathematische Methoden und Computereinsatz, die nach B. Taylor benannte Entwicklung einer Funktion in eine Potenzreihe um einen Entwicklungspunkt , wobei sich die Koeffizienten als Ableitungen der Funktion in  ergeben. Im einfachsten Fall einer skalar- und reellwertigen Funktion  mit stetigen Ableitungen -ter Ordnung auf dem kompakten Intervall  ergibt sich die Taylor-Reihe

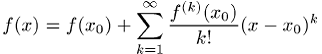
um einen Entwicklungspunkt  bzw. als Taylor-Reihe bis zur Ordnung

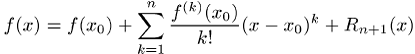
mit -ter Ableitung  und Lagrangeschem Restglied

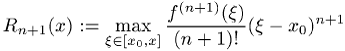
Die Taylor-Entwicklung ist genau dann möglich, wenn . Bemerkenswert ist, dass unter diesen Voraussetzungen  nur aus der Kenntnis von  und entsprechenden Ableitungen in  berechenbar ist. Wichtige Beispiele in der Physik sind die Taylor-Reihen der Funktionen

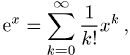
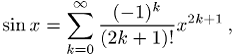
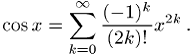
Der Konvergenzradius einer Taylor-Reihe folgt aus der Formel von Cauchy-Hadamard (Potenzreihe); anschaulich (Beispiel: Potenzreihe) ergibt sich der Konvergenzradius mit Mitteln der Funktionentheorie als Abstand von  bis zur nächsten Polstelle bzw. wesentlichen Singularität der Funktion .

Für eine reellwertige Funktion , die von einem Vektor  abhängt, nimmt die Taylor-Reihe die Gestalt

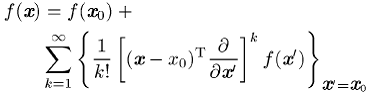
an. In der Physik werden häufig die Taylor-Reihen komplizierter Funktionen oder Ausdrücke nach dem linearen oder quadratischen Term abgebrochen; insbesondere die Linearisierung wie auch die Abschätzung von Fehler und Fehlerfortpflanzung basieren auf dieser Vorgehensweise.