Techniklexikon

Paramagnetismus

Elektrodynamik und Elektrotechnik, eine Form des Magnetismus, bei der ein Stoff ohne äusseres Magnetfeld H_ext kein messbares magnetisches Moment zeigt, in Anwesenheit eines äusseren Feldes jedoch eine Magnetisierung M erhält. Solche Materialien werden Paramagnetika genannt. Im Unterschied zum Diamagnetismus ist diese Magnetisierung gleichgerichtet zum äusseren Feld, verstärkt dieses also; ausserdem ist der Effekt betragsmässig wesentlich grösser. Dies liegt daran, dass im Gegensatz zu den Diamagnetika, bei denen durch das äussere Feld die mikroskopischen magnetischen Momente erst induziert werden (und nach der Lenzschen Regel ihrer Ursache entgegenwirken), die Paramagnetika über permanente mikroskopische Dipole verfügen, die vom äusseren Feld lediglich ausgerichtet werden. Auf Grund der thermischen Bewegung sind diese Dipole bei Paramagnetika bei Zimmertemperatur willkürlich verteilt, da die Wärmeenergie dann weitaus grösser als die zum Umklappen der Spins benötigte Energie ist. Bei tiefen Temperaturen können sich bei Paramagnetika verschiedene Ordnungszustände einstellen, die zu einem makroskopischen magnetischen Moment auch ohne äusseres Feld führen; umgekehrt zeigen ferromagnetische Substanzen, Antiferromagnetika und Ferrimagnetika oberhalb ihrer Curie-Temperatur (bzw. Néel-Temperatur) paramagnetisches Verhalten. Bei diesen Übergängen handelt es sich um Phasenübergänge zweiter Ordnung. Die magnetische Suszeptibilität von Paramagnetika ist nach dem Curie-Gesetz umgekehrt proportional zur Temperatur.

Die durchschnittliche Komponente der Magnetisierung in Richtung von H_ext ist nach der Langevinsche Formel L_¥(a) = cot a - 1 / a, a = mH_ext / kT, das Verhältnis aus magnetischer und thermischer Energie (m: atomares magnetisches Moment, k: Boltzmann-Konstante). Die Langevinsche Theorie des Paramagnetismus wendet hierfür die klassische Statistische Physik auf die Verteilung der atomaren Dipolrichtungen an. Dieses Ergebnis wird durch die Berücksichtigung der Richtungsquantisierung der Drehimpulse modifiziert. Es ergibt sich die von der Drehimpuls-Quantenzahl j abhängige, wesentlich kompliziertere Langevin-Funktion L_j(a), die für grosse j in die o.a. Formel übergeht (siehe Abb.).

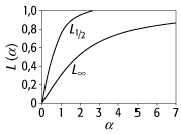
Paramagnetismus: Verlauf der klassisch (L_¥) und der quantenstatistisch für j = 1 / 2 (L_{1 / 2}) berechneten Langevin-Funktion.