Techniklexikon

Biegemoment

bei der Beschreibung der Biegung von Stäben das auf die neutrale Faser bezogene, resultierende Drehmoment M, das die Biegespannungen auf den Stabquerschnitt A ausüben: d. Nach der Bernoullischen Theorie (Biegung) sind die Biegespannungen zum senkrechten Abstand von der neutralen Schicht proportional, es ergibt sich deshalb für jedes Paar von Spannungen und Abständen s, z und ,  dasselbe Drehmoment (Abb.). Die Resultierende aller dieser infinitesimalen Momente ist das Biegemoment. Es hängt in der Regel von der Längenkoordinate x des Stabes ab und kann durch die Momentenfläche veranschaulicht werden: Das Biegemoment für jeden Querschnitt wird über der x-Koordinate desselben aufgetragen, und die Fläche zwischen der sich so ergebenden Momentenlinie und der Abszisse ist die Momentenfläche. In der Theorie der allgemeinen Biegung treten neben den Biegespannungen auch Querkräfte Q auf, die in Stäben mit dem Biegemoment gemäss  in Beziehung stehen.

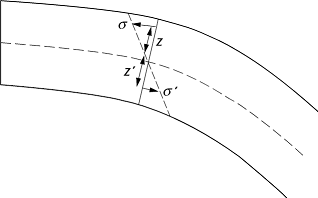
Biegemoment: Biegemoment senkrecht zur Achse eines gebogenen Stabes.