Legendre-Transformation

Petra Nordinghaus-Martin
spezielle
Koordinatentransformation, die z.B. in der klassischen Mechanik oder
Thermodynamik Anwendung findet. Gegeben sei eine Funktion ![]() zweier (skalarer oder vektorieller) Variablen x und y und ihr totales Differential
zweier (skalarer oder vektorieller) Variablen x und y und ihr totales Differential
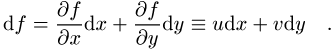
Mit Hilfe der Transformation ![]() erfolgt der Übergang auf die Differentiale du und dy gemäss
erfolgt der Übergang auf die Differentiale du und dy gemäss ![]() ; daraus
folgen die Identitäten
; daraus
folgen die Identitäten
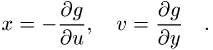
Man bemerkt, dass durch den Faktor ux
in der Transformation x als unabhängige Variable
eliminiert und durch u ersetzt wird. Beispiel: Das
totale Differential der Lagrange-Funktion in der klassischen Mechanik als
Funktion der Koordinaten q und Geschwindigkeiten ![]() ist
ist
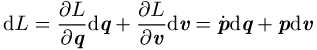
wegen ![]() und
und ![]() . Vermöge der
Transformation
. Vermöge der
Transformation ![]() gelangt man zum Differential
gelangt man zum Differential ![]() der Energie H, und
damit zu den Hamiltonschen Gleichungen (Analytische Mechanik)
der Energie H, und
damit zu den Hamiltonschen Gleichungen (Analytische Mechanik)
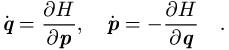
Techniklexikon.net
Das freie Technik-Lexikon. Fundierte Informationen zu allen Fachgebieten der Ingenieurwissenschaften, für Wissenschaftler, Studenten, Praktiker & alle Interessierten. Professionell dargeboten und kostenlos zugängig.
Techniklexikon
Modernes Studium der Physik sollte allen zugängig gemacht werden.