Techniklexikon

Laplace-Transformation

Integraltransformation, die besonders zur Lösung linearer gewöhnlicher Differentialgleichungssysteme geeignet ist. Solche treten z.B. auf bei der Analyse elektrischer Schaltkreise oder zur Beschreibung von Kompartment-Modellen in der Pharmakokinetik. Durch Anwendung der Laplace-Transformation wird das Differentialgleichungssystem in ein algebraisches Problem überführt; nach Lösung des algebraischen Problems und häufig nach Partialbruchzerlegungen wird mit Hilfe der inversen Laplace-Transformation die Lösung des ursprünglichen Differentialgleichungssystems konstruiert. Die Laplace-Transformation  einer stückweise stetigen, reell- oder komplexwertigen Funktion , die einer exponentiellen Wachstumbeschränkung  unterliegt, ist definiert als

 

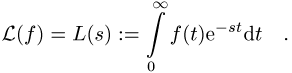
Entsprechend ist die inverse Laplace-Transformation definiert als . Wegen der Eigenschaften des Integrals ist auch  ein linearer Operator, d.h. es gilt

Nützlich ist auch die Verschiebungseigenschaft . Die Laplace-Transformation  der n-ten Ableitung einer Funktion  ist

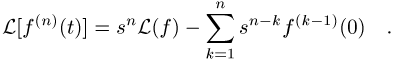
Die Laplace-Transformation eines Integrals ist dagegen

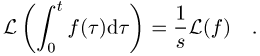
Die Eigenschaft

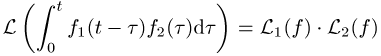
ist als Faltungssatz bekannt, d.h. wie bei der Fourier-Transformation entspricht dem Faltungsprodukt im ursprünglichen Bereich das gewöhnliche Produkt im Bildbereich. Schliesslich sei noch die Eigenschaft

genannt. Ist  eine für  holomorphe Funktion, konvergiert  gleichmässig bezüglich arg s, und ist das Integral  beschränkt, so ist  Laplace-Transformation der Funktion

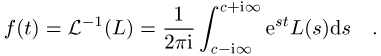
Der damit verbundene Integraloperator wird inverse Laplace-Transformation genannt.