Parsevalsche Gleichung

Karl-Wilhelm Steinfieber
OptikMathematische
Methoden und Computereinsatz, Abgeschlossenheitsrelation, Verschärfung der
Bessel-Ungleichung. Sei ![]() ein
abzählbares orthonormales Funktionensystem im Hilbert-Raum H. Die Bessel-Ungleichung garantiert, dass für jedes
ein
abzählbares orthonormales Funktionensystem im Hilbert-Raum H. Die Bessel-Ungleichung garantiert, dass für jedes ![]() die (verallgemeinerte)
Fourier-Reihe
die (verallgemeinerte)
Fourier-Reihe ![]() wieder
ein Element in H ist; die (verallgemeinerten)
Fourier-Koeffizienten
wieder
ein Element in H ist; die (verallgemeinerten)
Fourier-Koeffizienten ![]() sind
durch das Skalarprodukt
sind
durch das Skalarprodukt ![]() in
H gegeben, also
in
H gegeben, also ![]() . Ist die Parsevalsche Gleichung
. Ist die Parsevalsche Gleichung
![]()
erfüllt, so gilt ![]() . Ist
. Ist ![]() vollständig, so konvergiert
vollständig, so konvergiert ![]() für jedes
für jedes ![]() .
. ![]() heisst abgeschlossen, wenn die Parsevalsche
Gleichung für jedes
heisst abgeschlossen, wenn die Parsevalsche
Gleichung für jedes ![]() gilt,
und schliesslich ist die Abgeschlossenheit von
gilt,
und schliesslich ist die Abgeschlossenheit von ![]() äquivalent mit seiner Vollständigkeit. Die
Parsevalsche Gleichung lässt sich verallgemeinern auf nicht-abzählbare
orthonormale Funktionensysteme bzw. auf solche, die eine Vereinigung von
abzählbaren und nicht-abzählbaren Funktionensystemen darstellen; anstelle der
Reihe
äquivalent mit seiner Vollständigkeit. Die
Parsevalsche Gleichung lässt sich verallgemeinern auf nicht-abzählbare
orthonormale Funktionensysteme bzw. auf solche, die eine Vereinigung von
abzählbaren und nicht-abzählbaren Funktionensystemen darstellen; anstelle der
Reihe ![]() tritt dann
sinngemäss das Integral
tritt dann
sinngemäss das Integral ![]() bzw.
eine Summe aus Reihe und Integral auf, und die Parsevalsche Gleichung nimmt die
Gestalt
bzw.
eine Summe aus Reihe und Integral auf, und die Parsevalsche Gleichung nimmt die
Gestalt
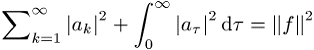
an.
In der Optik beschreibt die Parsevalsche Gleichung die Beziehung
zwischen einem abgestrahlten elektromagnetischen Feld f(t) bzw. der emittierten Energie und der spektralen
Energieverteilung F(w) als
Fourier-Transformierter von f(t), die emittierte Energie ist
proportional zu ![]() .
.
Erweitert man die Integrationsgrenzen, kann man mit
![]()
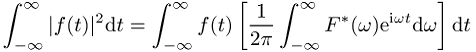
ausführen und erhält nach Vertauschen der Integrationsgrenzen die Parsevalsche Gleichung:
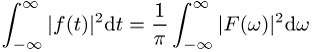
Techniklexikon.net
Das freie Technik-Lexikon. Fundierte Informationen zu allen Fachgebieten der Ingenieurwissenschaften, für Wissenschaftler, Studenten, Praktiker & alle Interessierten. Professionell dargeboten und kostenlos zugängig.
Techniklexikon
Modernes Studium der Physik sollte allen zugängig gemacht werden.