Techniklexikon

Nicht-Euklidizität

Relativitätstheorie und Gravitation, Eigenschaft einer zweidimensionalen, räumlichen Fläche, die dann gegeben ist, falls es unmöglich ist, einen Atlas aus kartesischen Koordinaten zu finden, welcher die gesamte Fläche überdeckt. Dies ist gleichbedeutend damit, dass es unmöglich ist, überall die Bedingung  erfüllt zu haben, wobei dr der Abstand zwischen zwei infinitesimal benachbarten Punkten ist und  die verwendeten Koordinaten sind. Statt dessen hat man , wobei die Einsteinsche Summenkonvention verwendet und die Notation  eingeführt wurde. Die Metrik  ist dann i. a. verschieden von der Einheitsmetrik . Anschaulich bedeutet dies, dass die Fläche gekrümmt ist. Es gelten in diesem Fall nicht mehr alle Axiome Euklids. So vermag die Winkelsumme in Dreiecken von  abzuweichen, und zu einer gegebenen Gerade kann es durch einen gegebenen Punkt mehr als eine oder überhaupt keine Parallele geben.

Da die Metrik nicht nur von der Krümmung der Fläche, sondern auch von den gewählten Koordinaten abhängt, kann man aus  nicht schliessen, dass die Fläche nicht-euklidisch ist. Verwendet man etwa Polarkoordinaten in der Ebene, so erhält man eine von der Einheitsmetrik verschiedene Metrik, obwohl die Fläche euklidisch ist. Um ein von den gewählten Koordinaten unabhängiges Kriterium für die (Nicht)-Euklidizität einer Fläche zu entwickeln, muss man aus der Metrik den Riemannschen Krümmungstensor berechnen. Die Fläche ist genau dann euklidisch, wenn dieser Tensor überall und mit all seinen Komponenten verschwindet.

Der Begriff Nicht-Euklidizität lässt sich sofort auf  höherdimensionale Räume übertragen. In der vierdimensionalen Raumzeit kann man dreidimensionale raumartige Hyperebenen betrachten und sie auf ihre Euklidizität hin untersuchen. Es kann durchaus vorkommen, dass diese euklidisch, also flach sind, obwohl die Raumzeit selbst gekrümmt ist. So ist beispielsweise ein homogen-isotropes Universum, welches durch eine  Robertson-Walker-Metrik

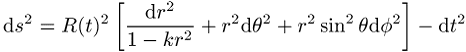
beschrieben wird, für alle Werte des Parameters  eine gekrümmte Raumzeit. Die durch t = const. definierten räumlichen Hyperflächen sind jedoch euklidisch, falls  ist. Auch der umgekehrte Fall ist denkbar (etwa bei nicht-flachen raumartigen Hyperflächen in der flachen Minkowski-Raumzeit).