Techniklexikon

ideale Gasgleichung

Thermodynamik und statistische Physik, Clapeyronsche Zustandsgleichung, Zustandsgleichung idealer Gase, lautet für alle idealen Gase gleichermassen:.

Hierbei sind p der Druck, V das Systemvolumen, N die Anzahl der Moleküle, k_B die Boltzmann-Konstante und T die absolute Temperatur.

Reale Gase lassen sich durch diese Zustandsgleichung um so besser beschreiben, je geringer ihre zwischenmolekularen Wechselwirkungen sind, bzw. wenn der Druck hinreichend klein gehalten wird. Das ideale Gas ist dann als Grenzzustand eines realen Gases mit verschwindenden Wechselwirkungen der Moleküle anzusehen. Zur mathematischen Beschreibung stellt man sich das Gasmolekül als Punktteilchen vor.

Im Gegensatz zur einheitlichen Form der idealen Gasgleichung werden reale Gase durch verschiedene Ansätze beschrieben, von denen die Van-der-Waals-Gleichung eine besonders einfache Form darstellt.

Anhand der idealen Gasgleichung lässt sich das Systemverhalten der Gase bei Zustandsänderung besonders einfach beschreiben und graphisch darstellen, insbesondere dann, wenn eine der Zustandsvariablen (p, T, V) konstant gehalten wird. Bei einer isobaren Zustandsänderung (p konstant, Isobare) besteht ein linearer Zusammenhang (graphisch eine Gerade) zwischen V und T. Ein solcher liegt auch zwischen p und T im Fall einer isochoren Zustandsänderung (V konstant, Isochore) vor. Der Zusammenhang zwischen p und V bei einer isothermen Zustandsänderung (T konstant, Isotherme) wird durch ein reziprokes Gesetz beschrieben (graphisch eine Hyperbel).

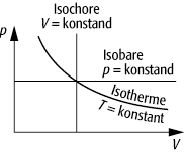
ideale Gasgleichung: Isotherme, Isobare und Isochore für ein ideales Gas im p-V-Diagramm.