Techniklexikon

Van-der-Waals-Gleichung

Thermodynamik und statistische Physik, Zustandsgleichung zur Beschreibung wesentlicher Eigenschaften realer Gase. Sie ist durch die Formel

gegeben. Sie unterscheidet sich von der Zustandsgleichung idealer Gase pv = RT durch eine Korrektur des Druckes und des Volumens.

Es ist p der Druck, v das molare Volumen, T die Temperatur und R die allgemeine Gaskonstante; die Konstanten a und b berücksichtigen Moleküleigenschaften der realen Gase: b das Eigenvolumen der Moleküle (Kovolumen) und der Ausdruck a / v² die gegenseitige Anziehung der Moleküle, wobei letztere Eigenschaft sich als zusätzlicher kleiner Druck auf die Gefässwände bemerkbar macht.

Die Van-der-Waals-Gleichung ermöglicht die Untersuchung von Phasenübergängen und kritischen Phänomenen realer Gase. Unter Zuhilfenahme der kritischen Zustandsgrössen für den Druck p_k, das molare Volumen v_k und der Temperatur T_k lässt sich die Van-der-Waals-Gleichung in den dimensionslosen reduzierten Grössen p_r = p / p_k, v_r = v / v_k, T_r = T / T_k aufschreiben:

Diese Gleichung ist von einer speziellen Substanz unabhängig. Betrachtet man unterschiedliche Substanzen bei denselben reduzierten Zustandsgrössen, so nennt man die zugehörigen Zustände korrespondierende Zustände. Die Gaskonstante ergibt sich daraus zu

Die experimentell bestimmten Werte R_exp unterscheiden sich jedoch vom theoretischen Wert oft beträchtlich; für CO₂ etwa ist R_exp / R » 0,73. Das liegt daran, dass die Van-der-Waals-Gleichung insbesondere am kritischen Punkt und im flüssigen Bereich die thermodynamischen Grössen quantitativ nicht richtig erfasst. Liegen die Phasen flüssig und gasförmig nebeneinander im Gleichgewicht vor, so erfolgt die Zustandsänderung zwischen diesen nicht entlang einer Isothermen, sondern entlang der Geraden , der Maxwell-Geraden (siehe Abb.), deren Verlauf durch das Maxwellsches Kriterium bestimmt wird.

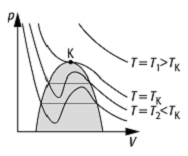
Van-der-Waals-Gleichung: p-V-Diagramm für eine Schar von Isothermen () und kritischer Punkt K. Im grau unterlegten Bereich findet der Phasenübergang flüssig–gasförmig statt. Die waagerechten Linien sind die Maxwellschen Geraden.