Techniklexikon

Einstein-Modell

Festkörperphysik, Einsteinsche Theorie der spezifischen Wärmekapazität, eine der ersten quantenmechanischen Theorien der Wärmekapazität von Festkörpern, die 1907 von A. Einstein entwickelt wurde. Grundlage der Theorie ist die Annahme, dass alle Atome des Festkörpers mit der gleichen Frequenz w_E, der Einstein-Frequenz, harmonisch und isotrop um ihre Gleichgewichtspositionen schwingen und ihre Bewegungen nicht korreliert sind. Das Modell beschreibt somit im wesentlichen optische Phononen (Phononen, optischer Zweig), und die Phononenzustandsdichte g(w) im Einstein-Modell ist eine d-Funktion:  (N: Anzahl der Elementarzellen, r: Anzahl der Atome in einer Elementarzelle). Die Schwingungsenergie E eines Kristalls ergibt sich im Einstein-Modell zu

wobei n(w) für die Besetzungswahrscheinlichkeit eines Zustands mit der Energie  nach der Bose-Einstein-Verteilung steht. Unter Verwendung der Einstein-Temperatur  erhält man für die Gesamtenergie genau das 3Nr-fache der Energie eines mit w_E schwingenden einzelnen harmonischen Oszillators:

(k_B: Boltzmann-Konstante). Die zugehörige spezifische Wärmekapazität c_V ergibt sich somit zu:

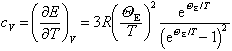
wobei R = N × k_B die allgemeine Gaskonstante bezeichnet. Für hohe Temperaturen (T >> Q_E) kann man die Exponentialfunktionen entwickeln und erhält mit c_V » 3 R das klassische Dulong-Petitsche Gesetz. Für niedrige Temperaturen (T << Q_E) ergibt sich wegen  für die Wärmekapazität. Hier geht deren Wert mit abnehmender Temperatur gegen null, folgt aber nicht der experimentell beobachteten T ³-Abhängigkeit (Debyesches T ³-Gesetz), die sich aus dem komplizierteren Debye-Modell ergibt. Hier zeigt sich der Näherungscharakter des Einstein-Modells, das exakt nur für zweiatomige Moleküle gilt, die als unabhängig schwingende Oszillatoren angesehen werden können. Trotz der sehr einfachen Annahmen beschreibt das Einstein-Modell die Wärmekapazitäten von Festkörpern relativ gut, insbesondere im Bereich hoher Temperaturen. [HW1]

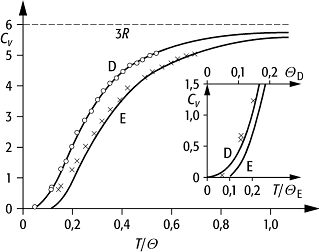
Einstein-Modell: Unterschiedliche Verläufe der Wärmekapazität (C_V) in Abhängigkeit von der Temperatur T im Debye-Modell (D) und im Einstein-Modell (E). R: allgemeine Gaskonstante, Q_D: Debye-Temperatur, Q_E: Einstein-Temperatur.