Techniklexikon

Ausströmgeschwindigkeit

Raketen motor die Geschwindigkeit, mit der Teilchen (z.B. Ladungspartikel, Verbrennungsprodukte usw.) eines Antriebsstrahls die Austrittsöffnung eines nach dem Rückstossprinzip funktionierenden Triebwerks verlassen. Prinzipiell ergibt sich die Ausströmgeschwindigkeit einer Treibstoffkombination aus der Umrechnung ihres Heizwertes in die Bewegungsenergie ihrer Verbrennungsgase. Dieser Wert ist allerdings ein theoretischer oberer Grenzwert und daher in der Realität mit ihren komplexen chemischen und thermodynamischen Abläufen nicht zu erreichen. Bedingt durch den Energieinhalt chemischer Treibstoffe liegt die durch Verbrennung maximal erreichbare Ausströmgeschwindigkeit bei knapp 7km/s.

Für praktische Anwendungen lässt sich die Höhe der Ausströmgeschwindigkeit _a nach folgender Formel berechnen:

,

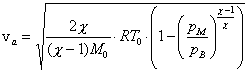wobei c das Verhältnis der spezifischen Wärmen und R die universelle Gaskonstante ist. Die Ausströmgeschwindigkeit hängt somit primär vom Verhältnis der Verbrennungstemperatur T₀ [K] zur molaren Masse M₀ der Arbeitsgase [kmol/kg] und erst sekundär vom Verhältnis des Düsenmündungsdrucks p_M zum Brennkammerdruck p_B ab.

Es empfiehlt sich demnach die Wahl von Treibstoffen, die bei möglichst hoher Temperatur verbrennen und deren Abgase eine möglichst niedrige Molmasse besitzen. Je kleiner das Verhältnis von Düsenmündungsdruck zu Brennkammerdruck ist, um so schneller verlassen die Verbrennungsgase die Düse. Dieser Sachverhalt erklärt auch, warum die Ausströmgeschwindigkeit des gleichen Triebwerks im Vakuum, in dem der Mündungsdruck gegen null geht, grösser ist als in der Atmosphäre, in der die Arbeitsgase nur bis auf 1bar herunter expandieren können. Raketen entwickeln also gerade im Vakuum einen besonders grossen Schub. Die höchste theoretisch erreichbare Ausströmgeschwindigkeit würde sich einstellen, wenn man die Triebwerke grundsätzlich für einen Betrieb im luftleeren Raum so auslegen könnte, dass die Arbeitsgase erst mit einem Düsenmündungsdruck p_M = 0 ins Freie austräten. Mehrere technische und physikalische Gründe verhindern dies jedoch. So wären beispielsweise extrem lange Entspannungsdüsen notwendig, die technisch jedoch nicht realisierbar sind. Auch muss verhindert werden, dass der jeweilige Düsenmündungsdruck unter den Aussendruck abfällt, weil es sonst zur sog. Strahlablösung kommen kann. Nicht zuletzt würde die Temperatur in der Düse im Vakuum unter den Verflüssigungs- bzw. Gefrierpunkt der Verbrennungsprodukte absinken, die dann nicht mehr als Gase vorlägen. Elektrische oder nukleare Raumantriebe ermöglichen höhere Ausströmgeschwindigkeiten. So rechnen Experten bei der Verwendung nuklearer Antriebe mit ungefähr 10, bei elektrothermischen Antrieben gar mit 20-100km/s. In diesen Fällen kann die Ausströmgeschwindigkeit für den Idealfall einer verlustlosen Strömung mit Hilfe der obigen Gleichung berechnet werden, da die thermodynamischen Bedingungen für das jeweilige Arbeitsmedium weitgehend identisch sind:

.

Für die Berechnung der Ausströmgeschwindigkeit elektrostatischer Antriebe kommt dagegen folgende Formel zum Einsatz:

,

wobei U die Beschleunigungsspannung, Q die Ladungsmenge und m die Ionenmasse darstellt. [SF]