Techniklexikon

Stabilitätsanalyse

Nichtlineare Dynamik, Chaos, Fraktale, Untersuchung der Stabilitätseigenschaften von Fixpunkten, periodischen Orbits, invarianten Mannigfaltigkeiten und anderen ausgezeichneten Mengen in der Theorie dynamischer Systeme. Als stabil wird dabei z.B. ein Fixpunkt bezeichnet, wenn es für jedes  ein  gibt, so dass Trajektorien, die in der -Umgebung des Fixpunktes starten, dessen -Umgebung nicht verlassen (siehe Abb. a). Ist der Fixpunkt sogar asymptotisch stabil, so existiert eine -Umgebung, aus der heraus alle Trajektorien auf den Fixpunkt zu laufen (siehe Abb. b). Bei der lokalen Stabilitätsanalyse werden nur Trajektorien in der unmittelbaren Umgebung der betreffenden Menge betrachtet und deren asymptotischer Verlauf mit Hilfe einer Linearisierung der Dynamik bestimmt. Globale Aussagen über das Einzugs- und Stabilitätsgebiet gewinnt man z.B. mit Hilfe geeigneter Ljapunow-Funktionen.

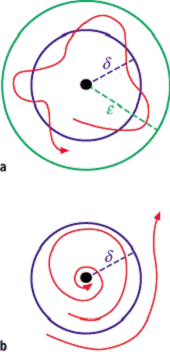
Stabilitätsanalyse: a) stabiler Fixpunkt, b) asymptotisch stabiler Fixpunkt.