Techniklexikon

Riemann-Cartan-Geometrie

Relativitätstheorie und Gravitation, Raumzeit-Mannigfaltigkeit mit nicht-verschwindender Torsion, die durch ihre Metrik  und den in ihren unteren Indizes nicht-symmetrischen Zusammenhangskoeffizienten cartan-geometrie.gif" alt="Riemann-Cartan-Geometrie"> definiert werden kann. Der antisymmetrische Teil der Zusammenhangskoeffizienten definiert den Torsionstensor , mit dem sich die Koeffizienten schreiben lassen als

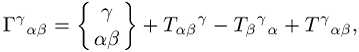
wobei  die Christoffel-Symbole der Riemannschen Geometrie sind. Geometrisch beschreibt der Torsionstensor die Abweichung davon, dass zwei infinitesimale Verschiebungsvektoren und ihre paralleltransportierten Vektoren auf einer Mannigfaltigkeit mit Torsion ein geschlossenes Parallelogramm bilden.