Techniklexikon

Phasenübergang zweiter Art

QuantenmechanikThermodynamik und statistische Physik, wird dadurch charakterisiert, dass die molare freie Enthalpie  und auch ihre erste Ableitung am Umwandlungspunkt stetig verläuft, während die zweite Ableitung von  dort eine Unstetigkeitsstelle aufweist. Im Gegensatz zum Phasenübergang erster Art tritt keine Umwandlungswärme auf. Ein Zugang zur Beschreibung ist die Landau-Theorie, die 1937 von L.D. Landau als phänomenologischer Zugang zur Beschreibung von Phasenübergängen 2. Art vorgeschlagen wurde. Sie benutzt das Konzept der Ordnungsparameter. Die Theorie gestattet, durch einen bei Annäherung an den Übergangspunkt verschwindenden Ordnungsparameter den Übergang zwischen den Phasen zu beschreiben, die am Phasenübergang selbst identisch, aber wegen unterschiedlicher Symmetrieeigenschaften dennoch durch einen scharfen Übergang voneinander getrennt sind. In der Theorie wird die freie Enthalpie G als Funktion von Temperatur T, Druck p und einem Ordnungsparameters u, der klassische fixierbar ist, aufgefasst. In der Vernachlässigung der Fluktuationen des Ordnungsparameters liegt die Begrenztheit der Landau-Theorie.

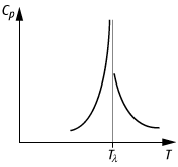
Die Abbildung veranschaulicht einen Phasenübergang zweiter Art am Beispiel der spezifischen Wärmekapazität , die am Umwandlungspunkt (l-Punkt) einen typischen l-förmigen Verlauf annimmt.

Beispiele für Phasenumwandlungen zweiter Art sind der Übergang von ferro- zu paramagnetischer Phase, der Übergang vom normalleitenden in den supraleitenden Zustand (ohne äusseres Magnetfeld), der Übergang von Ordnungs- zu Unordnungszuständen in Legierungen oder der Übergang zwischen festen Phasen (struktureller Phasenübergang).

Phasenübergang zweiter Art">

Phasenübergang zweiter Art: Beispiel an Hand des Verlaufs der molaren Wärme C_p in der Umgebung des l-Punktes.