Techniklexikon

Ladungsrenormierung

^[n] Teilchenphysik, Teil der quantenfeldtheoretischen Renormierungsprozedur (Renormierung), bei der die (zunächst bedeutungslosen) »nackten« Parameter e₀, m₀ der Lagrange-Dichte gerade so definiert werden, dass sie die bei der Berechnung von Strahlungskorrekturen auftretenden Divergenzen eliminieren, wodurch die physikalischen Parameter endlich werden. Im Fall der Quantenelektrodynamik treten insgesamt drei Typen von divergenten Graphen auf: die Selbstenergiegraphen von Elektron und Photon sowie der Elektron-Photon-Vertex. Sein Einschleifen-Diagramm (Feynman-Diagramm) führt auf die Vertexfunktion  mit dem Integral

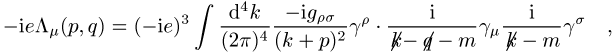
dessen Divergenz sich durch eine unendliche multiplikative Konstante Z₁ parametrisieren lässt:

Durch eine entsprechende Definition der unrenormierten Grösse e₀ kann der in 1/Z₁ steckende divergente Anteil des Vertexgraphen eliminiert werden. Dabei muss berücksichtigt werden, dass auch die äusseren Fermion- und Photonlinien des Vertex durch einen Faktor  renormiert werden müssen, so dass die renormierte Kopplungskonstante insgesamt

lautet. Mit Hilfe der Ward-Takahashi-Identitäten kann allerdings gezeigt werden, dass Z₁ = Z₂ ist, so dass sich die Bedingung an die renormierte Ladung auf  reduziert.