Techniklexikon

Kosterlitz-Thouless-Phasenübergang

Phasenübergang in zweidimensionalen Gittersystemen zwischen einer ungeordneten Phase mit exponentiell abfallenden Korrelationsfunktionen und einer schwach geordneten kritischen Phase mit algebraisch abfallenden Korrelationsfunktionen. Von besonderer Bedeutung ist dieser Phasenübergang beispielsweise im U(1)-Modell. Die freie Energie ist zwar unendlich oft stetig nach der Temperatur differenzierbar, bei der kritischen Temperatur T_c jedoch nicht analytisch. Die Korrelationslänge verhält sich für  wie

.

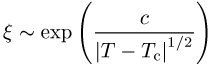Für  ist der Exponent des algebraischen Abfalls der Korrelationsfunktionen temperaturabhängig.

Physikalisch interpretiert man den Kosterlitz-Thouless-Phasenübergang im U(1)-Modell als Kondensation von Quasiteilchen, den sogenannten Vortex-Konfigurationen.