Techniklexikon

Debye-Relaxation

im Rahmen der Debyeschen Dipoltheorie entwickeltes Modell zur Beschreibung der dielektrischen Relaxation.

Die Debyesche Dipoltheorie geht von der Annahme aus, dass die kugelförmigen atomaren bzw. molekularen Dipole sich in einer Lösung der Viskosität h drehen können; diese Viskosität bremst die Dipolbewegung. Bei Anlegen eines elektrischen Feldes E strebt die Polarisation P stets mit einer durch die Relaxationszeit t charakterisierten Zeitverzögerung gegen den Gleichgewichtswert e₀(e_st - e _¥ )E:

 .

e _¥  ist der bei hohen Frequenzen allein wirksame Beitrag der Verschiebungspolarisation,  ist die statische Dielektrizitätskonstante, und e₀ ist die Dielektrizitätskonstante des Vakuums. Dieser Ansatz führt zu den Debye-Gleichungen für die Frequenzabhängigkeit der komplexen Dielektrizitätskonstanten e*(w) im Frequenzbereich der Orientierungspolarisation:

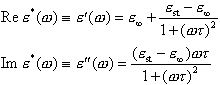
Unter Berücksichtigung der Wärmebewegung berechnet sich die Relaxationszeit im Rahmen der Debyeschen Dipoltheorie zu t = 4phr³/(k_BT) (r: Molekülradius, k_B: Boltzmann-Konstante, T: absolute Temperatur).

Mit dem Modell der Debye-Relaxation für e*(w) können wichtige Charakteristika realer dielektrischer Relaxationen gut reproduziert werden; der Frequenzverlauf von  weist bei w = t ^{- 1} eine Stufe von e_st nach e _¥  auf, während  bei der gleichen Frequenz ein Maximum durchläuft. Der dielektrische Verlust, charakterisiert durch den Verlustwinkel d, nimmt für Frequenzen w > t ^{- 1} gegenüber niedrigeren Frequenzen bedeutend zu:

Eine empirische Weiterentwicklung des Debyeschen Ansatzes ist das Modell der Havriliak-Negami-Relaxation.