Techniklexikon

Regelung

Elektronik, Halbleiterphysik, ein Verfahren, bei dem der vorgegebene Wert einer Grösse fortlaufend auf Grund von Messungen dieser Grösse mit einem Regler konstant gehalten wird. Der Regler muss auftretenden Störungen in geeigneter Weise entgegenwirken können. Ein Regelkreis (Schema siehe Abb. 1) ist ein geschlossenes System und besteht im einfachsten Fall aus der Regelstrecke und dem Regler. Der Regler bildet aus der Regeldifferenz, der Differenz zwischen der Regelgrösse und der Führungsgrösse, die Stellgrösse, die die Regelstrecke so beeinflusst, dass im Idealfall die Regeldifferenz verschwindet. Ebenso sollen die Veränderungen durch eine Störgrösse ausgeregelt werden. Die mathematische Behandlung der Regelung ist dann relativ einfach, wenn Regelstrecke und Regler lineare Systeme sind und der Regler ein stetiger Regler ist. In der Praxis sind diese Annahmen in vielen Fällen zumindest angenähert erfüllt.

Das statische Verhalten eines linearen Regelkreises kann durch die konstanten, im allgemeinen komplexen Übertragungsbeiwerte des Reglers (K_R) und der Regelstrecke (K_S) beschrieben werden. Für die Regelgrösse x in Abhängigkeit von der Führungsgrösse w und der Störgrösse z gilt:

Das dynamische Verhalten beschreibt die Vorgänge, wenn sich die von aussen wirkenden Einflüsse von w und z zeitlich ändern. Hierzu ist es günstig, in den Bildbereich der Laplace-Transformation überzugehen und das Regelsystem durch komplexe Übertragungsfunktionen darzustellen. Für die Frage nach der Stabilität eines Regelsystems ist das Produkt F_O = F_S F_R aus der Übertragungsfunktion F_S der Regelstrecke und der Übertragungsfunktion F_R des Reglers wichtig, das die Übertragungsfunktion des offenen Regelkreises genannt wird. Es tritt in der Berechnung der Führungsübertragungsfunktion (Reaktion auf Änderung der Führungsgrösse) und der Störübertragungsfunktion (Reaktion auf Störungen des Systems) in der Form 1 + F_O als Nennerterm auf, bestimmt also die Lage der Pole in der komplexen Frequenzebene. Liegen die Pole in der linken Halbebene, so ist das System stabil. Das hieraus abgeleitete Nyquist-Kriterium stellt F_O in der Abhängigkeit von der Frequenz als Ortskurve in der komplexen Ebene dar und besagt, dass ein System stabil ist, solange der Punkt -1 beim Durchlaufen der Ortskurve nicht umfahren wird. Die Art, wie weit sich die Ortskurve dem Punkt -1 nähert, wird durch die Grössen Phasenrand und Amplitudenrand beschrieben, woraus das Einschwingverhalten abgelesen werden kann. Ein anderes Stabilitätskriterium ist das Hurwitz-Kriterium, das von der Regelkreisgleichung im Zeitbereich ausgeht und an die Koeffizienten der zeitlichen Ableitungen der Regelgrösse bestimmte Bedingungen stellt. In der Praxis der Regelungstechnik versucht man, die Regelstrecke durch bekannte lineare Übertragungsglieder zu beschreiben und benutzt Standardregler. An Stelle dieser analogen Regler werden vermehrt digitale Regler eingesetzt, bei denen ein Prozessor die Regelalgorithmen realisiert.

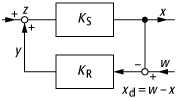
Regelung 1: Regelkreisschema (K_S: Regelstrecke, K_R: Regler, z: Störgrösse, y: Stellgrösse, x: Regelgrösse (Istwert), w: Führungsgrösse (Sollwert), x_d: Regeldifferenz).

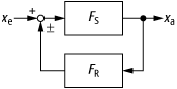
Regelung 2: Funktionsbild der Führungsübertragungsfunktion (F_S: Übertragungsfunktion der Regelstrecke, F_R: Übertragungsfunktion des Reglers, x_e: Regelgrösse am Eingang, x_a: Regelgrösse am Ausgang).