Techniklexikon

Newton-Verfahren

Mathematische Methoden und Computereinsatz, ein klassisches numerisches Iterationsverfahren zur näherungsweisen Berechnung der Lösungen (Wurzeln) der Gleichung  mit vielen Anwendungen in der numerischen Mathematik, den Natur- und Ingenieurwissenschaften und Verbindungen zu modernen mathematischen Gebieten, z.B. dem der Fraktale. Ist  eine approximative Lösung der Gleichung , so gewinnen Näherungsverfahren in der Regel eine verbesserte Lösung aus dem Iterationsschema

Die Verfahren unterscheiden sich darin, in welcher Weise  berechnet wird. Das klassische Newton-Verfahren geht von der Taylorreihenentwicklung der Funktion  um  aus und bricht dabei nach den Termen linearer Ordnung ab, d.h.

und ergibt mit der Forderung  für

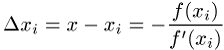
Bei Wahl eines geeigneten Startwertes kann das Verfahren konvergieren; wenn es konvergiert, so tut es dies mit quadratischer Konvergenzordnung, d.h. der Fehler  verhält sich wie

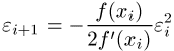
Anschaulich bedeutet dieses Fehlerverhalten, dass man im Falle der Konvergenz bei jedem Iterationsschritt zwei Dezimalstellen an Genauigkeit gewinnt. Die Fehlerformel zeigt aber auch, dass das Newton-Verfahren in der Umgebung lokaler Extremwerte (diese genügen der notwendigen Bedingung ) bzw. in der Nähe einer horizontalen Asymptote Konvergenzprobleme haben kann; hier kommt es entscheidend auf das Verhalten des Vorfaktors  an.

Das Newton-Verfahren lässt sich auf vektorwertige Gleichungssysteme  mit  und  erweitern;  wird dabei durch die Jacobi-Matrix  und  durch die Inverse  der Jacobi-Matrix ersetzt. Desweiteren findet das Newton-Verfahren in der Menge der komplexen Zahlen seine Fortsetzung (Identifizierung der komplexen Zahlenebene mit dem reellen Vektorraum ). Wendet man es auf die komplexe Polynomgleichung  an, so ergibt sich das Iterationsschema

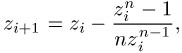
das wegen der Existenz von  nicht-notwendigerweise verschiedenen Nullstellen gegen maximal  verschiedene Lösungen konvergieren kann. Färbt man die Menge aller Anfangswerte, die gegen dieselbe Lösung  konvergieren, mit derselben Farbe ein, so ergibt sich ein Fraktal; wählt man die Farben je nach Zahl von Iterationen, die das Verfahren benötigt, um überhaupt zu konvergieren, so ergibt sich die Mandelbrotmenge, ein nunmehr klassisches Fraktal, das auch als Apfelmännchen bekannt ist.