Techniklexikon

Monte-Carlo-Simulation

Laserphysik und -technik, Berechnungsmethode mit Hilfe einer grossen Anzahl von zufälligen Zahlen. Sie wird hauptsächlich für Systeme mit sehr vielen Freiheitsgraden angewandt und fand erst mit der Verbreitung der Computertechnik Einzug in viele Bereiche der Mathematik, Physik und der technischen Wissenschaften, z.B. in der Theorie der Flüssigkeiten, bei der theoretischen Analyse von Solvatationseffekten und bei Konformationsberechnungen von Polymeren. Der Name der Methode wurde von Metropolis 1947 geprägt. Ein frühes Anwendungsbeispiel ist die Berechnung der Zahl p durch Buffon (1707-1788) mit einer grossen Zahl zufälliger Lagen einer Nadel der Länge l relativ zu einer Schar paralleler Geraden in der Ebene mit dem Abstand d > l. Damit erhält man eine experimentelle Abschätzung der Wahrscheinlichkeit, dass die Nadel eine Linie trifft, welche analytisch durch den Ausdruck 2l / (pd) gegeben ist (allerdings mit nur 4 Stellen Genauigkeit für » 10⁷ Versuche). Grössere Effizienz als bei dieser »Hit and Miss«-Methode erreicht man mit der Generation der Systemzustände nach der »Wichtigkeit«. Geeignete Aufgaben für dieses Herangehen sind z.B. Mittelwertberechnungen einer physikalischen Grösse A(r) von statistischen Ensembles

über alle Konfigurationen r; U(r) ist die potentielle Energie des Systems. Nur ein kleiner Teil des Konfigurationsraumes trägt wesentlich zum Integral bei, für die meisten Konfigurationen ist die Wahrscheinlichkeitsdichte  verschwindend klein. Nach der Methode von Metropolis bildet man eine Markowsche Kette, eine Folge  von Konfigurationen r_i im Konfigurationsraum, ausgehend von einer zufälligen Konfiguration r₀. Die Konfiguration r_{i + 1} bildet man auf der Basis von r_i nach folgender Regel: (1) r_i wird zufällig geändert, und eine Konfiguration r\' entsteht. (2) Falls ,so wird r_{i + 1} = r\' gesetzt. (3) Andernfalls wird  berechnet und mit einer zufälligen Zahl  verglichen. Es ist r_{i + 1} = r\', falls a < p. Bei allen verbleibenden Möglichkeiten ist r_{i + 1} = r_i. Mit Hilfe des Gesetzes der grossen Zahlen lässt sich beweisen, dass der arithmetische Mittelwert dieser Markowschen Kette im Sinne der Wahrscheinlichkeit gegen das Integral konvergiert

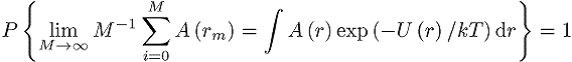
und damit die gewünschte Grösse  liefert. Die Monte-Carlo-Simulation mit ihrer Mittelung über das Ensemble ist prinzipiell äquivalent zur Molekulardynamik mit ihrer Mittelung über Zeiträume.