Techniklexikon

Methode der konjugierten Gradienten

iteratives Verfahren zur Minimierung einer Funktion . Es ist auch für sehr grosse numerische Probleme geeignet, da es sehr effizient arbeitet. Diese Methode ist eine Methode des steilsten Abstiegs, vermeidet aber den dort auftretenden »Zick-Zack-Kurs« bei der Annäherung an das lokale Minimum, indem sie sich dem lokalen Minimum in einer Richtung nähert, die konjugiert zur vorherigen, aber auch möglichst konjugiert zu allen übrigen Richtungen ist, in denen das Verfahren abstieg. Das Verfahren verwendet, beginnend mit einem beliebigen Vektor g₀ und  im Laufe der Iteration zwei Folgen von Vektoren

die, bei exakter Kenntnis der Hesse-Matrix , für  die folgenden Bedingungen für Orthogonalität und Konjugiertheit erfüllen:

 bezeichnet die Hesse-Matrix, d.h.

Damit ergeben sich die Skalare

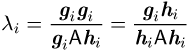
und

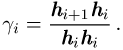
In der Praxis werden konjugierte Gradientenverfahren jedoch ohne Kenntnis von  und  ausgeführt. Statt dessen wird  durch den Gradienten  approximiert und der Vektor  als Suchrichtung in einem Liniensuchverfahren zur Bestimmung von  vom Punkt  ausgehend in Richtung  verwendet; sei  die Lösung dieses Liniensuchschritts, so wird  gesetzt und das Iterationsverfahren fortgeführt.