komplexe Zahlen

Hans-Peter Ahlsen
Mathematische
Methoden und Computereinsatz, eine Erweiterung des Körpers ![]() der reellen Zahlen, die insbesondere das
Rechnen mit Wurzeln aus negativen Zahlen ermöglicht. Die komplexen Zahlen
der reellen Zahlen, die insbesondere das
Rechnen mit Wurzeln aus negativen Zahlen ermöglicht. Die komplexen Zahlen ![]() bestehen aus Realteil
bestehen aus Realteil ![]() und Imaginärteil
und Imaginärteil ![]() , wobei
, wobei ![]() ist und lassen sich auf diese Weise in der
komplexen Zahlenebene (Gausssche Zahlenebene) isomorph zum Vektorraum
ist und lassen sich auf diese Weise in der
komplexen Zahlenebene (Gausssche Zahlenebene) isomorph zum Vektorraum ![]() abbilden. Der Körper
abbilden. Der Körper ![]() der komplexen Zahlen beinhaltet
der komplexen Zahlen beinhaltet ![]() als Unterkörper. Mit Hilfe der Eulerschen
Formel
als Unterkörper. Mit Hilfe der Eulerschen
Formel
![]()
lässt die Darstellung
der komplexen Zahlen in der komplexen Zahlenebene, die wiederum isomorph zum
Vektorraum ![]() ist, auch eine anschauliche geometrische Interpretation
im Sinne polarer Koordinaten zu:
ist, auch eine anschauliche geometrische Interpretation
im Sinne polarer Koordinaten zu: ![]() ist der Betrag der komplexen Zahl z bzw. des Vektors
ist der Betrag der komplexen Zahl z bzw. des Vektors ![]() und
und ![]() ist das Argument bzw. die Phase. Der Betrag
einer komplexen Zahl ist definiert als
ist das Argument bzw. die Phase. Der Betrag
einer komplexen Zahl ist definiert als
![]() ,
,
wobei ![]() die zu z
komplex-konjugierte Zahl genannt wird.
die zu z
komplex-konjugierte Zahl genannt wird. ![]() folgt für
folgt für ![]() aus
aus
![]()
Aus z und ![]() lassen sich vermöge der Definition von z und
lassen sich vermöge der Definition von z und ![]() Real- und Imaginärteil einfach darstellen als
Real- und Imaginärteil einfach darstellen als
![]() .
.
Gleichung (*) ermöglicht in einfacher Weise die Potenzierung komplexer Zahlen nach der Moivre-Formel
![]() . Die
Addition und Subtraktion komplexer Zahlen genügt den Rechenregeln
. Die
Addition und Subtraktion komplexer Zahlen genügt den Rechenregeln ![]() . Die
Multiplikation folgt aus dem Distributivgesetz unter Beachtung von
. Die
Multiplikation folgt aus dem Distributivgesetz unter Beachtung von ![]() :
:
![]() .
.
Die zu z inverse Zahl ![]() ist
ist ![]() , woraus die
Regel zur Division folgt:
, woraus die
Regel zur Division folgt:
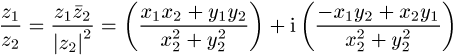 .
.
Techniklexikon.net
Das freie Technik-Lexikon. Fundierte Informationen zu allen Fachgebieten der Ingenieurwissenschaften, für Wissenschaftler, Studenten, Praktiker & alle Interessierten. Professionell dargeboten und kostenlos zugängig.
Techniklexikon
Modernes Studium der Physik sollte allen zugängig gemacht werden.