Techniklexikon

Carnotscher Kreisprozess

Carnot-Prozess, von S. Carnot 1824 entwickelter reversibler thermodynamischer Kreisprozess, der aus je zwei Isothermen und Adiabaten besteht. Der Carnotsche Kreisprozess bildet die theoretische Grundlage zur Berechnung des Wirkungsgrades aller (periodisch arbeitenden) Wärmekraftmaschinen. Ihm liegt folgendes Gedankenexperiment zugrunde: Die Arbeitssubstanz, für üblich ein Gas, befindet sich in einem Zylinder mit einem beweglichen Kolben und kann mit einem Thermostaten der absoluten Temperatur T₁ und einem weiteren Thermostaten der niedrigeren absoluten Temperatur T₂ Wärme austauschen. Es läuft nun ein Zyklus von vier Teilprozessen ab (Abb.):

1) Isotherme Expansion bei T = T₁: Die Substanz wird zunächst mit dem Wärmebehälter der Temperatur T₁ in Wärmekontakt gebracht und vergrössert dann bei der Expansion unter Arbeitsleistung ihr Volumen von V₁ auf V₂. Dabei wird einerseits dem Wärmebehälter die Wärme Q₁ entzogen und andererseits Arbeit nach aussen abgegeben.

2) Adiabatische Expansion: Die Substanz wird unter weiterer Arbeitsleistung so weit expandiert, bis sie sich auf die Temperatur T₂ abgekühlt hat.

3) Isotherme Kompression: Die Substanz wird mit dem Wärmebehälter der Temperatur T₂ in Wärmekontakt gebracht und unter Aufwendung äusserer Arbeit isotherm komprimiert. Dabei wird die Wärme Q₂ abgegeben.

4) Adiabatische Kompression: Die Substanz wird unter weiterer Aufwendung äusserer Arbeit komprimiert, bis sie die Temperatur T₁ wieder erreicht hat. Die Substanz befindet sich damit wieder in ihrem Anfangszustand.

Wesentlich ist, dass alle Prozesse reversibel ablaufen, d.h., sie können auch in umgekehrter Richtung verlaufen (Wärmepumpe, Kältemaschine).

Der Wirkungsgrad des Carnotschen Kreisprozesses, der Carnotsche Wirkungsgrad h_C, definiert als Quotient aus nach aussen abgegebener Arbeit und aufgenommener Wärme, lässt sich aus den ersten beiden Hauptsätzen der Thermodynamik berechnen: Nach dem ersten Hauptsatz muss die gewonnene Arbeit W = Q₁ - Q₂ sein. Wegen der Reversibilität des Prozesses gilt ausserdem nach dem zweiten Hauptsatz, dass sich insgesamt die Entropie nicht ändert, also . Diese Beziehung reduziert sich auf Q₁/T₁ - Q₁/T₂ = 0, da für die beiden adiabatischen Prozesse  gilt und die Isothermen in entgegengesetzter Richtung durchlaufen werden (: unvollständiges Differential). Die ausgetauschten Wärmemengen verhalten sich wie die zugeordneten absoluten Temperaturen. Damit erhält man für den Carnotschen Wirkungsgrad:

.

h_C ist also stets kleiner als eins; sein Wert ist unabhängig von der verwendeten Arbeitssubstanz. (Carnotsche Theoreme)

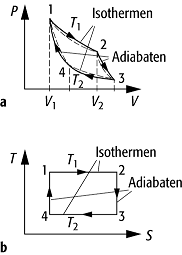
Carnotscher Kreisprozess: a) p,V-Diagramm des Carnotschen Kreisprozesses. p ist der Druck, den das Gas auf den Kolben ausübt, V das Gasvolumen. Die gestrichelten Kurven stellen einen realen Carnot-Prozess dar. Die umschlossene Fläche ist gleich der Arbeit , die bei einem Zyklus geleistet wird; b) besonders einfach lässt sich der Carnotsche Kreisprozess im T,S-Diagramm wiedergeben. T und S sind die Temperatur bzw. die Entropie des Gases. Die beiden Isothermen sind die beiden waagerechten Geraden T = T₁ und T = T₂, während die beiden Adiabaten durch die senkrechten Geraden (S = const.) dargestellt werden, da sich die Entropie S bei einem reversiblen adiabatischen Prozess nicht ändert.