Techniklexikon

Burgers-Vektor

Vektor zur Charakterisierung der Gitterverzerrungen einer Versetzung. Der Burgers-Vektor wird durch die Konstruktion eines Burgersumlaufes um das schlechte Kristallgebiet der Versetzung gewonnen: Man ordnet der Versetzung ein vollständig perfektes Kristallgebiet, den Bildkristall, zu. Alle Stellen des wirklichen Kristalls, denen man eindeutig entsprechende Stellen des Bildkristalls zuordnen kann, bezeichnet man als gutes Kristallgebiet, alle anderen, z.B. den Ort der Versetzung, als schlechtes. Zur Beschreibung der Versetzungsstärke umschreibt man die Versetzung im wirklichen Kristall durch einen nur im guten Gebiet verlaufenden geschlossenen Weg, den Burgers-Umlauf. Über die Festlegung des Richtungssinnes gibt es mehrere voneinander abweichende Konventionen. Der Vektor ist unabhängig von der Art der Erzeugung der Versetzung und von der Lage des Burgers-Umlaufes, wenn dieser vollständig in gutem Kristallgebiet verläuft. Der Burgers-Vektor eines mehrere Versetzungen umschliessenden Burgers-Umlaufes ist die Summe der Burgers-Vektoren der einzelnen Versetzungen. Umschreibt der Burgers-Umlauf eine unvollständige Versetzung, so kann er nicht vollständig im guten Kristallgebiet verlaufen. Er muss den mit der Versetzung verbundenen Stapelfehler schneiden. Man trifft dann über den Verlauf des Burgers-Umlaufes besondere Festlegungen. Im elastischen Kontinuum kann man den Burgers-Vektor durch das Linienintegral

längs eines geschlossenen Weges C um die Versetzung definieren, wobei u die elastischen Verschiebungen in dem die Versetzungen umgebenden Medium bedeutet.

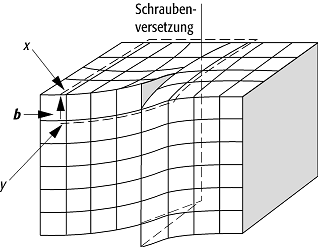
Burgers-Vektor: Der Burgers-Vektor b schliesst den Umlauf um eine Schraubenversetzung.