Techniklexikon

aperiodischer Grenzfall

die Situation, dass die Dämpfung eines schwingungsfähigen Systems gerade so gross ist, dass keine Oszillationen mehr auftreten wie beim Schwingfall, aber auch kein Kriechfall eintritt. In diesem Fall spricht man von kritischer Dämpfung. Bei einer gedämpften harmonischen Schwingung (Schwingung, freie) ist dies für  der Fall, wobei b die Dämpfungskonstante und  die Eigenfrequenz der ungedämpften Schwingung ist. Beim aperiodischen Grenzfall erreicht die Schwingung in der kürzestmöglichen Zeit ihre Ruhelage (s. Abb.), weshalb dieser Fall technisch sehr wichtig ist: z.B. sollen Stossdämpfer von Autos, Zeiger von analogen Messgeräten oder auch die Resonanzkörper von Musikinstrumenten möglichst schnell zur Ruhe kommen, weshalb sie auf aperiodische Dämpfung hin konstruiert werden.

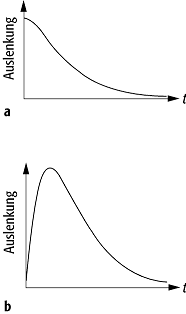
aperiodischer Grenzfall: Auslenkung beim aperiodischen Grenzfall. In Abb. a) ist x(0) ¹ 0, (0) = 0: der ausgelenkte Oszillator kehrt rasch in die Ruhelage zurück. In Abb. b) ist x(0) = 0 und (0) ¹ 0: der Oszillator wird in der Ruhelage angestossen und kehrt nach einer maximalen Auslenkung ebenfalls schnell in seine Ruhelage zurück.