zusammenhängend

Hans-Peter Ahlsen
Thermodynamik und statistische Physik, 1) Eigenschaft eines topologischen Raumes, wenn je zwei Punkte durch einen stetigen Weg miteinander verbunden werden können. Der topologische Raum heisst einfach zusammenhängend, wenn jeder geschlossene Weg stetig zu einem Punkt zusammengezogen werden kann. Anderenfalls bezeichnet man ihn als mehrfach zusammenhängend (siehe Abb.). Diese Eigenschaften von Mannigfaltigkeiten werden in der Homotopie-Theorie untersucht.
2) Eigenschaft von Graphen oder Clustern, wenn es zu je zwei Punkten eine Folge von benachbarten Punkten gibt, welche diese beiden Punkte verbindet. Ein Graph heisst einfach zusammenhängend, wenn es eine Linie gibt, deren Entfernung den Graphen in zwei nichtzusammenhängende Teile zerfallen lässt (bei Feynman-Graphen spricht man auch von Einteilchen-irreduziblen Graphen). Müssen mindestens N Linien entfernt werden, um den Graphen zerfallen zu lassen, so spricht man von N-fach zusammenhängend bzw. N-Teilchen-irreduziblen Graphen.
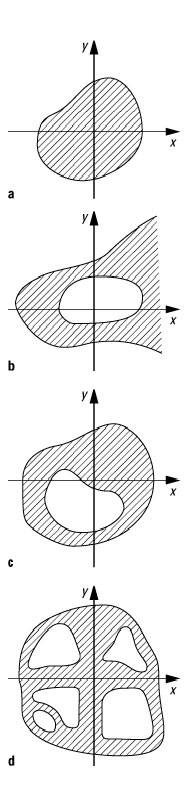
zusammenhängend: a) beschränktes einfach zusammenhängendes Gebiet, b) unbeschränktes zweifach zusammenhängendes Gebiet, c) beschränktes zweifach zusammenhängendes Gebiet, d) beschränktes mehrfach zusammenhängendes Gebiet.
Techniklexikon.net
Das freie Technik-Lexikon. Fundierte Informationen zu allen Fachgebieten der Ingenieurwissenschaften, für Wissenschaftler, Studenten, Praktiker & alle Interessierten. Professionell dargeboten und kostenlos zugängig.
Techniklexikon
Modernes Studium der Physik sollte allen zugängig gemacht werden.