Techniklexikon

Wärmeleitungsgleichung

Thermodynamik und statistische Physik, eine partielle Differentialgleichung zweiter Ordnung vom parabolischen Typ zur Beschreibung der Wärmeleitung durch die Temperaturverteilung  in Abhängigkeit vom Ort x und der Zeit t. Sie lautet für den allgemeinen anisotropen, inhomogenen Fall:

 

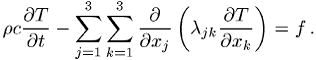
Hierbei sind die l_jk die Koeffizienten der positiv-definiten Wärmeleitfähigkeitsmatrix L, r die Materialdichte, c die spezifische Wärmekapazität und f die Wärmequellendichte.

Der homogene Fall ist durch die Quellenfreiheit  gekennzeichnet. Bei orthotroper Wärmeleitung besitzt L Diagonalgestalt, bei isotroper Wärmeleitung sind die Diagonalelemente gleich l, und es gilt . Im Fall  erhält man die stationäre Wärmeleitungsgleichung. Die Wärmeleitungsgleichung ist vom Gleichungstyp äquivalent zur Diffusionsgleichung (Diffusion).

Zur (numerischen) Lösung der Wärmeleitungsgleichung müssen entsprechende Rand- und Anfangsbedingungen angegeben werden. Anwendung findet sie in vielen technischen Bereichen.