Techniklexikon

Volterrasche Integralgleichung

Mathematische Methoden und Computereinsatz, Spezialfall einer linearen Integralgleichung mit variabler Integrationsgrenze. Gesucht ist die auf dem Intervall  definierte Funktion . Die Volterrasche Integralgleichung enthält einen von  abhängigen Integranden, z.B.

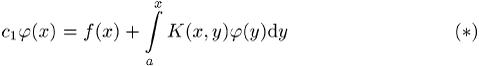
mit einer Störungsfunktion  und einem Kern  der Integralgleichung. Im Falle  spricht man von einer Volterraschen Integralgleichung erster Art. Als Spezialfall der Volterraschen Integralgleichung erster Art ergibt sich die Abelsche Integralgleichung mit  und , deren Kern für  unendlich wird. Die Volterrasche Integralgleichung erster Art kann durch Differentiation gelöst werden, wobei nach  als Parameter differenziert wird. Daraus ergibt sich

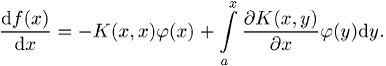
Lässt sich das Integral  geschickt durch  ausdrücken, so kann (*) in eine algebraische Bedingung für  umformuliert werden. Im Beispiel ,  und  ergibt sich so

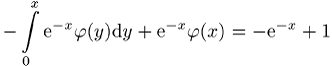
und daraus wegen  schliesslich . Handelt es sich bei dem Kern  um ein Polynom in  und  vom Grade , so verschwindet wegen  der Integralterm nach -maligem Differenzieren und hinterlässt eine gewöhnliche Differentialgleichung -ter Ordnung in .