Techniklexikon

Spannungs-Dehnungs-Diagramm

Klassische Mechanik, Spannungs-Dehnungs-Kurve, Diagramm, das entsteht, wenn man im Zugversuch die Zugspannung s = F / A am Probekörper über seiner relativen Längenänderung e = Dl / l aufträgt. Es ist zu bemerken, dass die aufgetragene Spannung vereinbarungsgemäss auf den Anfangsquerschnitt des Probekörpers bezogen wird, obwohl sich dieser auf Grund der Querkontraktion verringert. Die aufgetragene Spannung ist demnach kleiner als die tatsächlich anliegende. Aus diesem Diagramm können dann verschiedene Parameter des elastischen Verhaltens des Probekörpers abgelesen werden.

Bei kleinen Längenänderungen sind e und s zueinander proportional, man bezeichnet diesen Abschnitt als Hookesche Gerade (Hookesches Gesetz). Ab der Proportionalitätsgrenze s_P (siehe Abb.) ändert sich die Steigung der Kurve, die Spannung wächst nun langsamer an. Nach Verringern der Zugkraft, die Spannungen bis zur Höhe der Dehngrenze s_D erzeugt, kehrt der Körper auf seine Ausgangslänge zurück. Ein über die Dehngrenze hinaus belasteter Körper behält nach Entspannung Längenänderungen bei. Auf mikroskopischer Ebene setzt in Metallen ab der Dehngrenze ein plastisches Fliessen der Kristallite (»Körner«) ein, deshalb wird s_D auch als Fliessgrenze bezeichnet.

Bei weiterer Erhöhung der Zugkraft nimmt die Längenänderung pro Zugeinheit weiter ab. Der Körper verformt sich plastisch, wobei er sich langsam verfestigt. Ab der Elastizitätsgrenze s_E erreicht er seine höchste Festigkeit, die Zugfestigkeit. Bei weiterer Erhöhung der Kraft nimmt die Spannung ab, weil der Körper der angelegten Kraft kaum noch Widerstand bieten kann. Der Querschnitt des Probekörpers schnürt sich ein bis zum Zerreissen bei der Bruchspannung s_B.

Es ist mit fundamentalen Methoden der theoretischen Physik praktisch aussichtslos, für ein bestimmtes Material den Kurvenverlauf im Spannungs-Dehnungs-Diagramm vorherzusagen. Man behilft sich zur Beschreibung von Materialeigenschaften daher mit heuristischen Spannungs-Dehnungs-Beziehungen.

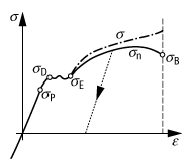
Spannungs-Dehnungs-Diagramm: Kurve für das Beispiel des Stahls, das eine ausgeprägte Dehngrenze besitzt. Die ausgezogene Linie stellt die auf den Ursprungsquerschnitt bezogene Nennspannung s_n, die strichpunktierte Linie die auf den wirklichen Querschnitt bezogene Realspannung dar. Oberhalb von s_E erfolgt Rückfederung längs der punktierten Linie; s_P: Proportionalitätsgrenze, s_F: Dehngrenze, s_E: Elastizitätsgrenze, s_B: Bruchspannung.