Techniklexikon

regula falsi

Mathematische Methoden und Computereinsatz, nicht sehr effizientes numerisches Näherungsverfahren zur Bestimmung der Lösungen der Gleichung , das nur auf Funktionswerten von f aufbaut. Ersetzt man im Newton-Verfahren die Ableitung bzw. Tangente durch den Differenzenquotienten bzw. die Sekante, so erhält man mit gegebenen Startwerten  und  das (zweistufige) Sekantenverfahren

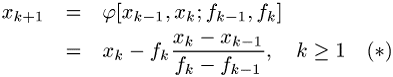
mit  und . Wegen der Auslöschung im Differenzenquotienten wird dieses Verfahren in der Nähe der Nullstelle  leicht instabil. Wählt man jedoch die Startwerte  und , so dass , d.h. Funktionswerte verschiedenen Vorzeichens (für stetige Funktionen impliziert dies nach dem Zwischenwertsatz die Existenz einer Nullstelle von f im Intervall ), iteriert dann gemäss

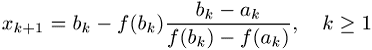
und setzt

so erhält man das unter dem Namen regula falsi bekannte Verfahren, welches stabil und mit linearer Konvergenzordnung gegen eine Nullstelle  konvergiert. Dieses Verfahren ist hinsichtlich der Konvergenzeigenschaft aber nur so gut wie das Bisektionsverfahren, in dem man die Nullstelle durch Intervallhalbierung bestimmt. Eine Verbesserung der regula falsi ergibt sich bei Abwandlung des Sekantenverfahrens durch das Illinois-Verfahren:

1) gegeben seien Startwerte  und  mit ;

2) berechne  und ;

3) Vorzeichentest

a) falls , so berechne ,

b) falls  so berechne ;

4) wiederhole 2) mit .

Das Verfahren ist so konstruiert, dass  in jedem Schritt erfüllt ist und die Berechnung von  in 2) ermöglicht.