Oberflächenrekonstruktionen

Hans-Peter Ahlsen
Oberflächen- und Grenzflächenphysik
Einleitung
Wird ein Kristall,
dessen Inneres sich durch eine regelmässige Anordung von atomaren Bausteinen
beschreiben lässt, durch eine Oberfläche terminiert, kommt es zumeist zu einer
Umordnung der Atome der Oberfläche, die man als Rekonstruktion bezeichnet. Das
kristalline Gitter des dreidimensionalen Kristalls (des Substrats) wird
gebildet durch die Translation der Basis, die aus einer beliebigen Anzahl von
verschiedenen Atomen (für die einfachsten Kristalle aus nur einem) bestehen
kann, und damit kann jeder Punkt ![]() des Gitters mit Hilfe der Gittervektoren
des Gitters mit Hilfe der Gittervektoren ![]() und dreier ganzer Zahlen
und dreier ganzer Zahlen ![]() in der Form
in der Form ![]() beschrieben werden. Kristalle ohne
Translationsinvarianz sind von dieser Betrachtung ausgenommen. Eine Oberfläche
wird bezeichnet durch
beschrieben werden. Kristalle ohne
Translationsinvarianz sind von dieser Betrachtung ausgenommen. Eine Oberfläche
wird bezeichnet durch ![]() , wobei die
reziproken Werte der Millerschen Indizes, d.h.
, wobei die
reziproken Werte der Millerschen Indizes, d.h. ![]() , die
Schnittpunkte der Fläche mit den von den Gittervektoren
, die
Schnittpunkte der Fläche mit den von den Gittervektoren ![]() definierten Achsen bezeichnen. Diese ideale
Oberfläche kann (bei unveränderter Basis) durch zwei neue
Oberflächengittervektoren
definierten Achsen bezeichnen. Diese ideale
Oberfläche kann (bei unveränderter Basis) durch zwei neue
Oberflächengittervektoren ![]() beschrieben werden, plus einem geeigneten
Vektor
beschrieben werden, plus einem geeigneten
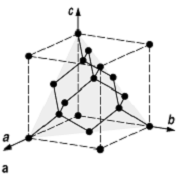
Vektor ![]() normal zur Oberfläche. [56]Abbildung 1 zeigt dies als Beispiel
für die Diamantstruktur und deren (111)-Fläche. Eine solche Oberfläche, die die
Anordnung von Atomen innerhalb einer Ebene im Kristall widerspiegelt, kann man
jedoch selten beobachten; es kommt überwiegend zur Zerstörung dieser alten
Ordnung in der Oberfläche. Stellt sich eine neue Ordnung ein, bezeichnet man
diese als Rekonstruktion.
normal zur Oberfläche. [56]Abbildung 1 zeigt dies als Beispiel
für die Diamantstruktur und deren (111)-Fläche. Eine solche Oberfläche, die die
Anordnung von Atomen innerhalb einer Ebene im Kristall widerspiegelt, kann man
jedoch selten beobachten; es kommt überwiegend zur Zerstörung dieser alten
Ordnung in der Oberfläche. Stellt sich eine neue Ordnung ein, bezeichnet man
diese als Rekonstruktion.
Die rekonstruierte
Oberfläche ist durch eine neue Basis und meist durch eine grössere Einheitszelle
gekennzeichnet. Diese kann durch die Vektoren ![]() und
und ![]() und die Rekonstruktion somit durch die Matrix
und die Rekonstruktion somit durch die Matrix
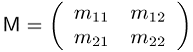
charakterisiert
werden. Vereinfachend wird meist die Woodsche Notation verwendet, und eine
Rekonstruktion wird durch ![]() bezeichnet, wobei
bezeichnet, wobei ![]() ,
, ![]() mit
mit ![]() ,
, ![]() und
und ![]() der Winkel zwischen
der Winkel zwischen ![]() und
und ![]() ist. Diese Notation ist am gebräuchlichsten,
aber nicht zur Beschreibung aller Rekonstruktionen gut geeignet.
ist. Diese Notation ist am gebräuchlichsten,
aber nicht zur Beschreibung aller Rekonstruktionen gut geeignet.
Ursachen der Oberflächenrekonstruktion
Die Struktur der
Oberfläche wird diktiert durch die Forderung, dass die freie Energie ![]() minimal ist. Für das Auftreten einer
Rekonstruktion an einer Oberfläche gibt es auch ohne den Einfluss der Entropie S bei Temperaturen
minimal ist. Für das Auftreten einer
Rekonstruktion an einer Oberfläche gibt es auch ohne den Einfluss der Entropie S bei Temperaturen ![]() mehrere Gründe, unabhängig davon, ob es sich
um einen metallischen, kovalenten oder ionischen Kristall handelt: (1) Den
Oberflächenatomen fehlen Bindungsnachbarn, was ihre innere Energie
mehrere Gründe, unabhängig davon, ob es sich
um einen metallischen, kovalenten oder ionischen Kristall handelt: (1) Den
Oberflächenatomen fehlen Bindungsnachbarn, was ihre innere Energie ![]() gegenüber dem Volumen stark erhöht. Die
ungesättigten Oberflächenbindungen (»dangling bonds«) werden durch die
Rekonstruktion zumindest zum Teil abgesättigt, womit
gegenüber dem Volumen stark erhöht. Die
ungesättigten Oberflächenbindungen (»dangling bonds«) werden durch die
Rekonstruktion zumindest zum Teil abgesättigt, womit ![]() wieder sinkt. (2) Die Stöchiometrie der
Oberfläche ist gegenüber dem Volumen geändert. Das Abdampfen (Desorption) eines
Elementes eines mehrelementigen Kristalls oder die Anlagerung (Adsorption) von
Fremdatomen führen, meist begleitet von Umordnung der Oberflächenatome des
Substrats, zur Rekonstruktion. (3) Die Gleichgewichtsgitterkonstante
wieder sinkt. (2) Die Stöchiometrie der
Oberfläche ist gegenüber dem Volumen geändert. Das Abdampfen (Desorption) eines
Elementes eines mehrelementigen Kristalls oder die Anlagerung (Adsorption) von
Fremdatomen führen, meist begleitet von Umordnung der Oberflächenatome des
Substrats, zur Rekonstruktion. (3) Die Gleichgewichtsgitterkonstante ![]() der Oberfläche, d.h. die Gitterkonstante, die
die Oberfläche einnehmen würde, wäre sie frei vom Substrat, »passt nicht« zur
Gitterkonstanten
der Oberfläche, d.h. die Gitterkonstante, die
die Oberfläche einnehmen würde, wäre sie frei vom Substrat, »passt nicht« zur
Gitterkonstanten ![]() des Substrats. Für die Gitterfehlanpassung
des Substrats. Für die Gitterfehlanpassung ![]() gilt
gilt ![]() mit einer ganzen Zahl
mit einer ganzen Zahl ![]() und
und ![]() . Dies ist
nach der Adsorption von Fremdatomen der Fall, tritt aber auch für reine
Oberflächen auf.
. Dies ist
nach der Adsorption von Fremdatomen der Fall, tritt aber auch für reine
Oberflächen auf.
Die Rekonstruktion reiner Oberflächen am Beispiel von Si(111) und Ge(111)
Silicium und Germanium
kristallisieren in der Diamantstruktur, deren Einheitszelle in [57]Abb. 1a gezeigt ist. Die Struktur ist
bestimmt durch die Rehybridisierung der vier atomaren 3s2 3p2
(4s2 4p2)-Orbitale von Si (Ge) zu vier sp3-Hybridorbitalen
mit einer symmetrischen, tetraedrischen Struktur. Diese sind zu Bändern
(Bändermodell) verbreitert, dem vollständig mit Elektronen gefüllten Valenzband
und dem unbesetzten Leitungsband, die, für Halbleiter typisch, durch eine
Energielücke voneinander getrennt sind.
Erzeugen wir eine
(111)-Fläche wie in [58]Abb. 1a angedeutet, z.B. durch Spalten
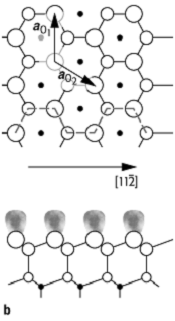
eines Kristalls, so weist jedes Atom dieser Oberfläche, die schematisch in [59]Abb. 1b gezeigt ist, ein halbgefülltes
sp3-Orbital auf. Diese »dangling bond«-Zustände sind metallisch,
liegen innerhalb der Energielücke des Kristalls und sind instabil gegenüber
einem Peierls-Übergang: Die Oberflächeneinheitszelle verdoppelt ihre Grösse, und
das halbbesetzte (metallische) Band spaltet auf in ein besetztes, das
energetisch abgesenkt wird, und ein unbesetztes, das energetisch angehoben
wird, womit ![]() sinkt und sich auch an der Oberfläche wieder
eine Energielücke auftut. Dieser Mechanismus wurde ursprünglich für ein
eindimensionales Metall postuliert und hat grosse Bedeutung für die
Rekonstruktion von Halbleiteroberflächen. Durch Spalten erzeugte (111)-Flächen
von Si und Ge bilden eine
sinkt und sich auch an der Oberfläche wieder
eine Energielücke auftut. Dieser Mechanismus wurde ursprünglich für ein
eindimensionales Metall postuliert und hat grosse Bedeutung für die
Rekonstruktion von Halbleiteroberflächen. Durch Spalten erzeugte (111)-Flächen
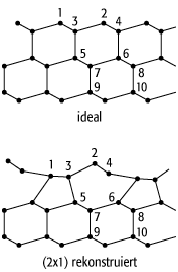
von Si und Ge bilden eine ![]() -Rekonstruktion,
wie in [60]Abb. 2 schematisch gezeigt. Die Atome 1
der rekonstruierten Oberfläche sind sp3-hybridisiert mit einem voll
besetzten »dangling bond«-Zustand, während die Atome 2 eine
-Rekonstruktion,
wie in [60]Abb. 2 schematisch gezeigt. Die Atome 1
der rekonstruierten Oberfläche sind sp3-hybridisiert mit einem voll
besetzten »dangling bond«-Zustand, während die Atome 2 eine ![]() Hybridisierung (wie Graphit) aufweisen, wobei
das
Hybridisierung (wie Graphit) aufweisen, wobei
das ![]() Orbital unbesetzt ist.
Orbital unbesetzt ist.
Gestattet man
Materialtransport, also Diffusion auf der Oberfläche (z.B. durch Tempern),
bildet sich für Si(111) eine ![]() - und für
Ge(111) eine
- und für
Ge(111) eine ![]() -Rekonstruktion
aus, die die energetisch günstigsten Strukturen von
-Rekonstruktion
aus, die die energetisch günstigsten Strukturen von ![]() bis weit oberhalb der Raumtemperatur sind. Die
Energien beider Rekonstruktionen, d.h.
bis weit oberhalb der Raumtemperatur sind. Die
Energien beider Rekonstruktionen, d.h. ![]() und
und ![]() , sind auf
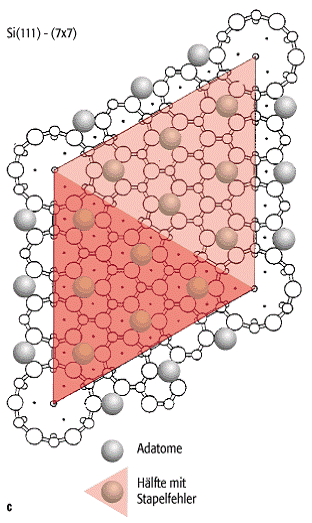
beiden Flächen, d.h. Si(111) und Ge(111), sehr ähnlich. [61]Abb. 3 zeigt Modelle,
Rastertunnelmikroskop- und Elektronenbeugungsbilder dieser Strukturen.
Zentraler Baustein bei beiden sind die sogenannten Adatome, d.h. zusätzliche
Atome, die auf der (111)-Fläche an jeweils drei Oberflächenatome gebunden sind.
, sind auf
beiden Flächen, d.h. Si(111) und Ge(111), sehr ähnlich. [61]Abb. 3 zeigt Modelle,
Rastertunnelmikroskop- und Elektronenbeugungsbilder dieser Strukturen.
Zentraler Baustein bei beiden sind die sogenannten Adatome, d.h. zusätzliche
Atome, die auf der (111)-Fläche an jeweils drei Oberflächenatome gebunden sind.
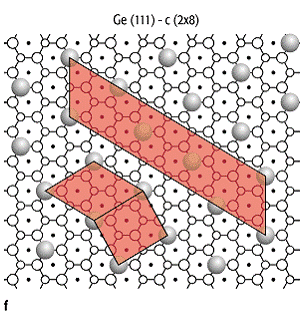
Bei der Ge(111)-c(![]() )-Rekonstruktion
sind diese in »Streifen« abwechselnd in (
)-Rekonstruktion
sind diese in »Streifen« abwechselnd in (![]() )- und c(
)- und c(![]() )-Anordnung
angelagert (siehe [62]Abb. 3e und [63]Abb. 3f). Für jedes Adatom gibt es
genau ein sogenanntes Restatom, das an kein Adatom gebunden ist. Damit besässen
Adatom und Restatom jeweils eine freie Valenz, d.h. einen halbgefüllten
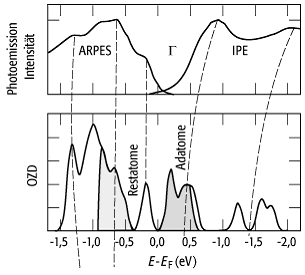
»dangling bond«-Zustand. [64]Abb. 4 zeigt für Ge(111)-
)-Anordnung
angelagert (siehe [62]Abb. 3e und [63]Abb. 3f). Für jedes Adatom gibt es
genau ein sogenanntes Restatom, das an kein Adatom gebunden ist. Damit besässen
Adatom und Restatom jeweils eine freie Valenz, d.h. einen halbgefüllten
»dangling bond«-Zustand. [64]Abb. 4 zeigt für Ge(111)-![]() gemessene
und berechnete Zustandsdichten, die auch für diese Struktur den
Peierls-Mechanismus qualitativ bestätigen: Durch Ladungstransfer sind die
Adatomzustände nahezu unbesetzt, die Restatomzustände nahezu vollständig
besetzt und die elektronische Oberflächenzustandsdichte (OZD) in der Nähe des
Ferminiveaus
gemessene
und berechnete Zustandsdichten, die auch für diese Struktur den
Peierls-Mechanismus qualitativ bestätigen: Durch Ladungstransfer sind die
Adatomzustände nahezu unbesetzt, die Restatomzustände nahezu vollständig
besetzt und die elektronische Oberflächenzustandsdichte (OZD) in der Nähe des
Ferminiveaus ![]() , wie man in
[65]Abb. 4 sehen kann, sehr gering. Die
, wie man in
[65]Abb. 4 sehen kann, sehr gering. Die ![]() -Oberfläche
erniedrigt die
-Oberfläche
erniedrigt die ![]() -Symmetrie
der Ge(111)-Fläche, und es bleibt lediglich die Translationsinvarianz (
-Symmetrie
der Ge(111)-Fläche, und es bleibt lediglich die Translationsinvarianz (![]() -Symmetrie).
-Symmetrie).
Die Si(111)-![]() -Rekonstruktion
ist etwas komplizierter; eine Hälfte der Einheitszelle weist einen Stapelfehler
auf, und die beiden Hälften der Einheitszelle sind durch eine Reihe von Dimeren
verbunden, wodurch für Si(111) die Spannungsenergie in der Oberfläche
verringert wird. Die Grösse der Einheitszellen von Si(111)-(
-Rekonstruktion
ist etwas komplizierter; eine Hälfte der Einheitszelle weist einen Stapelfehler
auf, und die beiden Hälften der Einheitszelle sind durch eine Reihe von Dimeren
verbunden, wodurch für Si(111) die Spannungsenergie in der Oberfläche
verringert wird. Die Grösse der Einheitszellen von Si(111)-(![]() ) und
Ge(111)-c(
) und
Ge(111)-c(![]() ) hat es
bedingt, dass von ihrer ersten Entdeckung im Jahre 1959 durch R.E. Schlier und
H.E. Farnsworth bis zu ihrer Entschlüsselung etwa 25 Jahre vergingen.
) hat es
bedingt, dass von ihrer ersten Entdeckung im Jahre 1959 durch R.E. Schlier und
H.E. Farnsworth bis zu ihrer Entschlüsselung etwa 25 Jahre vergingen.
Kommensurable, diskommensurable und inkommensurable Rekonstruktionen
Die Bedeutung der
Gitterfehlanpassung ![]() für die Strukturbildung an Oberflächen soll an
Hand eines eindimensionalen Modells nach Frenkel & Kontorova (Phys. Z. SU 13,
1 (1938)) bzw. Frank & van der Merwe (Proc. Royal Soc. London 189,
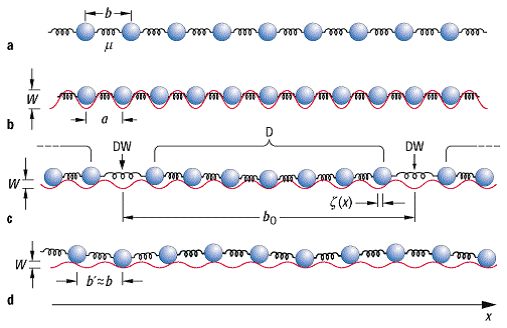
205 (1949)) verdeutlicht werden (siehe [66]Abb. 5). Das Substrat ist durch das
periodische Potential
für die Strukturbildung an Oberflächen soll an
Hand eines eindimensionalen Modells nach Frenkel & Kontorova (Phys. Z. SU 13,
1 (1938)) bzw. Frank & van der Merwe (Proc. Royal Soc. London 189,
205 (1949)) verdeutlicht werden (siehe [66]Abb. 5). Das Substrat ist durch das
periodische Potential ![]() repräsentiert. Ohne die Wechselwirkung
repräsentiert. Ohne die Wechselwirkung ![]() mit dem Substrat hat das Adsorbat A die
Gitterkonstante b, die mit Hilfe der
»Federkonstanten«
mit dem Substrat hat das Adsorbat A die
Gitterkonstante b, die mit Hilfe der
»Federkonstanten« ![]() eingestellt wird ([67]Abb. 5a).
eingestellt wird ([67]Abb. 5a).
Ist ![]() stark und
stark und ![]() schwach, fallen die Adsorbatatome einfach in
die Mulden des Substratpotentials, das Substrat bestimmt die Gitterkonstante
des Adsorbats, es ist kommensurabel ([68]Abb. 5b). Für den allgemeinen
zweidimensionalen Fall bedeutet dies, dass alle Matrixelemente von
schwach, fallen die Adsorbatatome einfach in
die Mulden des Substratpotentials, das Substrat bestimmt die Gitterkonstante
des Adsorbats, es ist kommensurabel ([68]Abb. 5b). Für den allgemeinen
zweidimensionalen Fall bedeutet dies, dass alle Matrixelemente von ![]() ganze Zahlen sind.
ganze Zahlen sind.
Ist ![]() schwach und
schwach und ![]() stark, nimmt das Adsorbat auch auf der
Oberfläche (nahezu) seine eigene Gitterkonstante
stark, nimmt das Adsorbat auch auf der
Oberfläche (nahezu) seine eigene Gitterkonstante ![]() an, und das Adsorbat ist inkommensurabel ([69]Abb. 5d). Für den zweidimensionalen
Fall kann die Inkommensurabilität in nur einer oder auch in zwei Raumrichtungen
vorliegen, d.h. dass mindestens ein Matrixelement
an, und das Adsorbat ist inkommensurabel ([69]Abb. 5d). Für den zweidimensionalen
Fall kann die Inkommensurabilität in nur einer oder auch in zwei Raumrichtungen
vorliegen, d.h. dass mindestens ein Matrixelement ![]() von
von ![]() keine ganze Zahl ist.
keine ganze Zahl ist.
Wenn weder ![]() noch
noch ![]() dominieren, passt sich das Adsorbat innerhalb
von Domänen D nahezu der Gitterkonstanten der idealen Oberfläche an. Wie in [70]Abb. 5c gezeigt, gerät das Adsorbat
aber vom Zentrum der Domäne aus zunehmend ausser Phase mit dem Substratgitter.
An der Domänenwand DW, die man auch als Diskommensuration bezeichnet, geht die
Phasenbeziehung vollständig verloren. Man kann der entstandenen Rekonstruktion
die neue Gitterkonstante
dominieren, passt sich das Adsorbat innerhalb
von Domänen D nahezu der Gitterkonstanten der idealen Oberfläche an. Wie in [70]Abb. 5c gezeigt, gerät das Adsorbat
aber vom Zentrum der Domäne aus zunehmend ausser Phase mit dem Substratgitter.
An der Domänenwand DW, die man auch als Diskommensuration bezeichnet, geht die
Phasenbeziehung vollständig verloren. Man kann der entstandenen Rekonstruktion
die neue Gitterkonstante ![]() zuordnen, wobei im gezeigten eindimensionalen
Beispiel die Basis aus sieben Atomen besteht. Nicht zuletzt auf Grund der
Verminderung der freien Energie
zuordnen, wobei im gezeigten eindimensionalen
Beispiel die Basis aus sieben Atomen besteht. Nicht zuletzt auf Grund der
Verminderung der freien Energie ![]() durch die Zunahme der Entropie bei
durch die Zunahme der Entropie bei ![]() flukturieren die Domänen einer
diskommensurablen Rekonstruktion meist in ihrer Grösse. Die Rekonstruktion ist
also nicht periodisch, kann nur durch eine mittlere Gitterkonstante beschrieben
werden, und die Matrixelemente
flukturieren die Domänen einer
diskommensurablen Rekonstruktion meist in ihrer Grösse. Die Rekonstruktion ist
also nicht periodisch, kann nur durch eine mittlere Gitterkonstante beschrieben
werden, und die Matrixelemente ![]() von
von ![]() , bzw. die
Faktoren
, bzw. die
Faktoren ![]() für die Woodsche Notation, sind grosse (
für die Woodsche Notation, sind grosse (![]() ),
nichtrationale Zahlen.
),
nichtrationale Zahlen.
Inkommensurable und
diskommensurable Rekonstruktionen entstehen meist nach Adsorption von Fremdatomen,
werden aber auch in einigen Fällen für reine Oberflächen beobachtet. Eingehend
experimentell und theoretisch untersucht wurden in der Vergangenheit
Oberflächen, die im Grundzustand (![]() )
kommensurabel sind und mit der Temperatur über die Zwischenstufe der
Diskommensurabilität, wobei man die Diskommensurationen als thermische
Anregungen des Systems verstehen kann, inkommensurabel werden. Diese stetigen
Phasenübergänge (zweiter Ordnung) werden beispielsweise für Edelgase auf
Graphit oder Metalloberflächen beobachtet.
)
kommensurabel sind und mit der Temperatur über die Zwischenstufe der
Diskommensurabilität, wobei man die Diskommensurationen als thermische
Anregungen des Systems verstehen kann, inkommensurabel werden. Diese stetigen
Phasenübergänge (zweiter Ordnung) werden beispielsweise für Edelgase auf
Graphit oder Metalloberflächen beobachtet.
Adsorbatbedeckte Oberflächen
Kommensurable Rekonstruktionen
Rekonstruktionen, die
sich nach der Adsorption von Fremdatomen ausbilden, sind in erster Linie
dadurch geprägt, dass das Adsorbat (= Oberflächenatome des Substrats plus die
Fremdatome) bestrebt ist, freie Bindungen zu vermeiden. Ein dreiwertiges
Ga-Atom kann drei freie Valenzen der (111)-Fläche von Si oder Ge absättigen,
und mit einer Belegung von 1 / 3 Monolage (1 Monolage (ML) = 1 Atom pro Substrat-Oberflächenatom)
Ga sind alle »dangling bonds« besetzt. In der Tat ist die Si(111)-Oberfläche
mit 1 / 3 ML Ga (auf Si(111), 1 ML = 7,84 ´ 1014 Atome × cm-2) vollständig ![]() -rekonstruiert.
Dabei sind die Ga-Atome an drei Oberflächenatome direkt über einem weiteren
Si-Atom in der zweiten Lage gebunden. Trotz der vollständigen chemischen
Passivierung der (111)-Fläche ist die Si(111)-
-rekonstruiert.
Dabei sind die Ga-Atome an drei Oberflächenatome direkt über einem weiteren
Si-Atom in der zweiten Lage gebunden. Trotz der vollständigen chemischen
Passivierung der (111)-Fläche ist die Si(111)-![]() -Rekonstruktion
energetisch nicht sehr günstig. Die tetraedrischen Bindungswinkel (120°) des Si
müssen stark verbogen werden, und diese Spannungsenergie erhöht
-Rekonstruktion
energetisch nicht sehr günstig. Die tetraedrischen Bindungswinkel (120°) des Si
müssen stark verbogen werden, und diese Spannungsenergie erhöht ![]() so sehr, dass die Struktur auf Si(111) marginal
stabil ist und auf Ge(111) nicht beobachtet wird.
so sehr, dass die Struktur auf Si(111) marginal
stabil ist und auf Ge(111) nicht beobachtet wird.
Diskommensurable Rekonstruktionen
Auf Ge(111) (und auf
Si(111) für Bedeckungen >1/3 ML) substituiert Ga für die Oberflächenatome der
(111)-Fläche und liefert genau die drei Valenzelektronen für die Bindungen zur
nächsttieferen Atomlage. Da aber der kovalente Radius von Ga mit 0,126 nm
deutlich grösser ist als der von Si (0,117 nm) und Ge (0,123 nm) und die
Oberfläche von sp3
zu der Graphit-ähnlichen ![]() -Hybridisierung
wechselt, ist die Gleichgewichtsgitterkonstante des Adsorbats wesentlich grösser
als die der idealen (111)-Fläche. Zudem sind die Bindungen des GeGa
(SiGa)-Adsorbats zu der nächsttieferen Ge (Si)-Schicht deutlich geschwächt. Als
Folge bildet sich eine diskommensurable Rekonstruktion, wie die
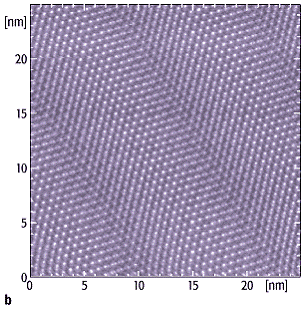
Rastertunnelmikroskopie-Bilder der b-Phase von Ge(111):Ga in [71]Abb. 6 zeigen. Man sieht ein
nichtperiodisches Netzwerk von Domänen ([72]Abb. 6a), in dessen Innerem ein Gitter
mit einer gegenüber der idealen Ge(111)-Fläche um 8% vergrösserten
Gitterkonstanten sichtbar ist ([73]Abb. 6b).
-Hybridisierung
wechselt, ist die Gleichgewichtsgitterkonstante des Adsorbats wesentlich grösser
als die der idealen (111)-Fläche. Zudem sind die Bindungen des GeGa
(SiGa)-Adsorbats zu der nächsttieferen Ge (Si)-Schicht deutlich geschwächt. Als
Folge bildet sich eine diskommensurable Rekonstruktion, wie die
Rastertunnelmikroskopie-Bilder der b-Phase von Ge(111):Ga in [71]Abb. 6 zeigen. Man sieht ein
nichtperiodisches Netzwerk von Domänen ([72]Abb. 6a), in dessen Innerem ein Gitter
mit einer gegenüber der idealen Ge(111)-Fläche um 8% vergrösserten
Gitterkonstanten sichtbar ist ([73]Abb. 6b).
Inkommensurable Rekonstruktionen
Mit 1 / 3 ML Belegung
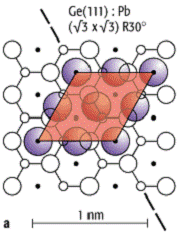
bildet Pb auf Ge(111) eine ![]() -Rekonstruktion
wie Ga auf Si(111) und mit 4 / 3 ML-Belegung eine
-Rekonstruktion
wie Ga auf Si(111) und mit 4 / 3 ML-Belegung eine ![]() -Rekonstruktion,
wie in [74]Abb. 7a gezeigt mit vier Atomen pro
Einheitszelle. Erhöht man die Pb-Belegung weiter, rücken die Pb-Atome normal zu
der in [75]Abb. 7a eingezeichneten gestrichelten
Linie dichter zusammen, und die Rekonstruktion wird inkommensurabel. Wie [76]Abb. 5d schematisch zeigt, sind
inkommensurable Adsorbate durch das Substrat moduliert. Regionen, quasi
Domänen, in denen sich das Adsorbat nahezu in den Potentialmulden des Substrats
befindet (dunkle Streifen in [77]Abb. 7b), wechseln sich ab mit
Regionen, quasi Domänenwänden (helle Regionen in [78]Abb. 7b), in denen sich das Adsorbat
nahe der Maxima des Potentials befindet. Es entsteht ein Moiré-Muster, wie das
Rastertunnelmikroskop-Bild in [79]Abb. 7b deutlich zeigt. Der
Streifenabstand nimmt mit zunehmender Pb-Belegung bis zu einem Wert von etwa 5
nm ab.
-Rekonstruktion,
wie in [74]Abb. 7a gezeigt mit vier Atomen pro
Einheitszelle. Erhöht man die Pb-Belegung weiter, rücken die Pb-Atome normal zu
der in [75]Abb. 7a eingezeichneten gestrichelten
Linie dichter zusammen, und die Rekonstruktion wird inkommensurabel. Wie [76]Abb. 5d schematisch zeigt, sind
inkommensurable Adsorbate durch das Substrat moduliert. Regionen, quasi
Domänen, in denen sich das Adsorbat nahezu in den Potentialmulden des Substrats
befindet (dunkle Streifen in [77]Abb. 7b), wechseln sich ab mit
Regionen, quasi Domänenwänden (helle Regionen in [78]Abb. 7b), in denen sich das Adsorbat
nahe der Maxima des Potentials befindet. Es entsteht ein Moiré-Muster, wie das
Rastertunnelmikroskop-Bild in [79]Abb. 7b deutlich zeigt. Der
Streifenabstand nimmt mit zunehmender Pb-Belegung bis zu einem Wert von etwa 5
nm ab.
Für Ge(111):PB sind
Kreuzungen der Streifen/Domänenwände energetisch ungünstig, sie verlaufen parallel.
Eine hexagonal inkommensurable Phase, wie in [80]Abb. 7c gezeigt, bildet sich, wenn Kreuzungen
von Domänenwänden energetisch begünstigt sind/werden, was für Ge(111):Pb nur
durch eine Erhöhung der Konzentration von Defekten erreicht wird.
Oberflächenrekonstruktionen
1: a) Die Einheitszelle der Diamantstruktur in der C, Si, Ge, und ![]() -Sn
kristallisieren. Die (111)-Ebene ist schattiert. b) Die (111)-Ebene in Aufsicht
(oben) und Seitenansicht (unten) mit angedeuteten »dangling bonds«. Der Schnitt
erfolgt entlang der in der Aufsicht eingezeichneten gestrichelten Linie.
-Sn
kristallisieren. Die (111)-Ebene ist schattiert. b) Die (111)-Ebene in Aufsicht
(oben) und Seitenansicht (unten) mit angedeuteten »dangling bonds«. Der Schnitt
erfolgt entlang der in der Aufsicht eingezeichneten gestrichelten Linie. ![]() ,
, ![]() ,
, ![]() mit der kubischen Gitterkonstante
mit der kubischen Gitterkonstante ![]() .
.
Oberflächenrekonstruktionen
2: Die (![]() )-Rekonstruktion
von Si(111) und Ge(111), die sich nach Herstellen einer (111)-Fläche durch das
Spalten eines Kristalls ausbildet. Gezeigt ist ein Querschnitt der (111)-Fläche
für die unrekonstruierte, ideale (oben) und die rekonstruierte Oberfläche
(unten).
)-Rekonstruktion
von Si(111) und Ge(111), die sich nach Herstellen einer (111)-Fläche durch das
Spalten eines Kristalls ausbildet. Gezeigt ist ein Querschnitt der (111)-Fläche
für die unrekonstruierte, ideale (oben) und die rekonstruierte Oberfläche
(unten).
Oberflächenrekonstruktionen
3: Die Rekonstruktionen der getemperten (111)-Oberflächen von Si (aO = 0,384 nm) und Ge (aO
= 0,400 nm). a)-c) Si(111)-(![]() ) (bO = 2,69 nm). d)-f) Ge(111)-c(
) (bO = 2,69 nm). d)-f) Ge(111)-c(![]() ) (
) (![]() = 0,80 nm,
= 0,80 nm, ![]() = 3,2 nm). a), d) Elektronenbeugungsbilder,
b), e) Rastertunnelmikroskopie-Abbildungen; die Abbildungsbedingungen sind so
gewählt, dass nur die Adatome sichtbar sind; Bild b): 8,85 nm, Bild e): 9,7 nm.
c), f) Modelle der Rekonstruktionen in Aufsicht.
= 3,2 nm). a), d) Elektronenbeugungsbilder,
b), e) Rastertunnelmikroskopie-Abbildungen; die Abbildungsbedingungen sind so
gewählt, dass nur die Adatome sichtbar sind; Bild b): 8,85 nm, Bild e): 9,7 nm.
c), f) Modelle der Rekonstruktionen in Aufsicht.
Oberflächenrekonstruktionen
4: Die elektronische Oberflächenzustandsdichte (OZD) von Ge(111)--c(![]() ) (am G-Punkt, d.h.,
Elektronenimpuls normal zur Oberfläche), wie sie sich aus Messungen (oben) und
Rechnungen (unten) ergibt. ARPES = Winkelaufgelöste
Photoelektronenspektroskopie; IPE = Inverse Photoelektronenspektroskopie.
) (am G-Punkt, d.h.,
Elektronenimpuls normal zur Oberfläche), wie sie sich aus Messungen (oben) und
Rechnungen (unten) ergibt. ARPES = Winkelaufgelöste
Photoelektronenspektroskopie; IPE = Inverse Photoelektronenspektroskopie.
Oberflächenrekonstruktionen
5: Gitterfehlanpassung ![]() und Rekonstruktion. a) Freies Adsorbat mit
Gleichgewichtsgitterkonstante
und Rekonstruktion. a) Freies Adsorbat mit
Gleichgewichtsgitterkonstante ![]() und »Federkonstante«
und »Federkonstante« ![]() . b)-d)
Adsorbat auf Substrat: b) kommensurables Adsorbat auf Substrat, c)
diskommensurables Adsorbat; Domänen D sind durch Diskommensurationen DW (=
Domänenwände) getrennt. d) Inkommensurables Adsorbat.
. b)-d)
Adsorbat auf Substrat: b) kommensurables Adsorbat auf Substrat, c)
diskommensurables Adsorbat; Domänen D sind durch Diskommensurationen DW (=
Domänenwände) getrennt. d) Inkommensurables Adsorbat.
Oberflächenrekonstruktionen
6: Rastertunnelmikroskopische Abbildung einer diskommensurablen Rekonstruktion
von Ge(111) für ca. 0,8 Monolagen Ga-Belegung. Im oberen Teil des Bildes sieht
man in einem grösseren Ausschnitt die nichtperiodische Struktur von Domänen und
Domänenwänden mit einer Grösse der Oberflächeneinheitszelle von 12-15 ![]() (4,8-6 nm). Im unteren Teil sieht man das
Innere der Domänen mit einer Gitterkonstanten von 1,08
(4,8-6 nm). Im unteren Teil sieht man das
Innere der Domänen mit einer Gitterkonstanten von 1,08 ![]() (
(![]() = 0,4 nm)
und die Diskommensurationen mit hoher Auflösung.
= 0,4 nm)
und die Diskommensurationen mit hoher Auflösung.
Oberflächenrekonstruktionen
7: Rekonstruktionen von Blei auf Ge(111). a) Die Einheitszelle der Ge(111):Pb-![]() -Phase
(Sättigungsbelegung, 4 / 3 ML) mit 4 Atomen. b) Die inkommensurable
»Streifenphase« für eine Pb-Belegung von 1,4 Monolagen. c) Die inkommensurable
hexagonale Phase von Pb auf Ge(111), die durch Defekte stabilisiert wird.
-Phase
(Sättigungsbelegung, 4 / 3 ML) mit 4 Atomen. b) Die inkommensurable
»Streifenphase« für eine Pb-Belegung von 1,4 Monolagen. c) Die inkommensurable
hexagonale Phase von Pb auf Ge(111), die durch Defekte stabilisiert wird.
Techniklexikon.net
Das freie Technik-Lexikon. Fundierte Informationen zu allen Fachgebieten der Ingenieurwissenschaften, für Wissenschaftler, Studenten, Praktiker & alle Interessierten. Professionell dargeboten und kostenlos zugängig.
Techniklexikon
Modernes Studium der Physik sollte allen zugängig gemacht werden.