Techniklexikon

harmonische Funktionen

skalare, stetige und mindestens zweifach stetig differenzierbare Funktionen U(x,y,...) mehrerer Variablen x, y, ..., die der Laplace-Gleichung

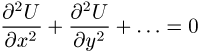
genügen. Kennt man die Werte einer harmonischen Funktion auf einer geschlossenen Fläche, so sind auch die Werte in allen inneren Punkten des von der Fläche umschlossenen Gebietes bekannt. Die harmonischen Funktionen sind in der Feldtheorie (z.B. in der Elektrodynamik) von Bedeutung.