Hamilton-Dichte

Petra Nordinghaus-Martin
Dichte, als deren Integral die Hamilton-Funktion für kontinuierliche Systeme
oder Felder definiert werden kann. Um eine Hamilton-Dichte einzuführen, muss man
die Feldkoordinaten mit einiger Strenge definieren. Dazu wird der Raum in
infinitesimale Zellen unterteilt. Zu jeder Zelle gehört eine Systemkoordinate j
dr. Der zu dieser Koordinate konjugierte Impuls p
ist üblicherweise durch die Funktionalableitung der Lagrange-Funktion L nach der Geschwindigkeitskomponente ![]() gegeben. Die Hamilton-Dichte
gegeben. Die Hamilton-Dichte ![]() wird definiert mit einem Integralausdruck
wird definiert mit einem Integralausdruck ![]() . Die
entsprechenden Hamilton-Gleichungen haben dann allerdings nicht mehr die
einfache Gestalt der kanonischen Form, sondern lauten:
. Die
entsprechenden Hamilton-Gleichungen haben dann allerdings nicht mehr die
einfache Gestalt der kanonischen Form, sondern lauten: ![]() und
und
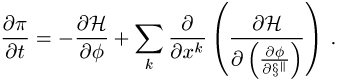
Techniklexikon.net
Das freie Technik-Lexikon. Fundierte Informationen zu allen Fachgebieten der Ingenieurwissenschaften, für Wissenschaftler, Studenten, Praktiker & alle Interessierten. Professionell dargeboten und kostenlos zugängig.
Techniklexikon
Modernes Studium der Physik sollte allen zugängig gemacht werden.