Chaos

Hans-Peter Ahlsen
Das ursprünglich
altgriechische Wort Chaos (caoV) bezeichnet die gestaltlose Urmasse, aus
der die Erde (altgriechisch Gaia bzw. Gaia) entstand. Heute
verstehen wir unter Chaos ganz allgemein einen ungeordneten, schwer
vorhersagbaren Zustand, wir sprechen z.B. vom "Verkehrschaos".
Während dieses Bild das Zusammenspiel von vielen Verkehrsteilnehmern, welchen
in der Chaostheorie viele Freiheitsgrade entsprechen, beschreibt, zeigte sich
in jüngster Zeit, dass auch Systeme mit wenigen Freiheitsgraden, wie etwa ein
periodisch getriebenes Pendel, chaotisches Zeitverhalten zeigen können. Dies
bedeutet, dass seine Winkelposition als Funktion der Zeit irregulär und auf
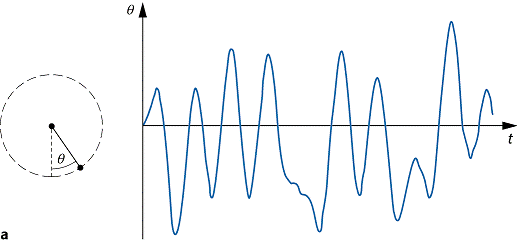
lange Sicht unvorhersagbar wird ([1]Abb. 1a). Diese Art von Chaos
bezeichnet man als deterministisches Chaos.
Der Schmetterlingseffekt
Zunächst erscheint der Begriff "deterministisches Chaos" als ein Widerspruch in sich selbst, da das Unvorhersagbare nicht determiniert "sein kann". Dieser scheinbare Widerspruch erklärt sich folgendermassen: Obwohl das Zeitverhalten des Pendels durch Differentialgleichungen vollständig beschrieben wird, aus denen sich Schritt für Schritt die Trajektorie berechnen lässt, benötigt man doch zum Finden einer Lösung die Kenntnis der Anfangsbedingungen.
Systeme, die
deterministisches chaotisches Verhalten zeigen, haben die Eigenschaft, dass
kleine Abweichungen in den Anfangsbedingungen sich im Laufe der Zeit
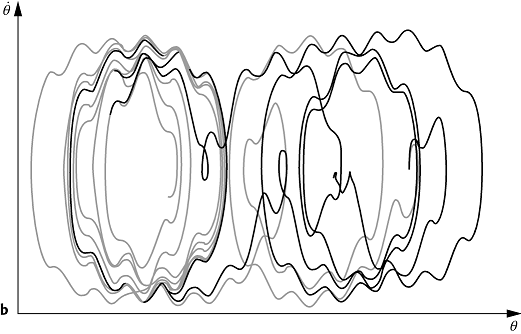
exponentiell verstärken ([2]Abb. 1b). Der Meteorologe E.N. Lorenz
hat dafür das Wort "Schmetterlingseffekt" geprägt; damit ist gemeint,
dass der Flügelschlag eines Schmetterlings in Rio de Janeiro im Prinzip auch das
Wetter in Berlin beeinflussen kann. Da die Anfangsbedingungen experimentell
stets nur mit endlicher Genauigkeit bekannt sein können, es also immer einen
"Anfangsfehler" gibt, führt die Verstärkung dieses Anfangsfehlers
dazu, dass die Systeme langfristig unvorhersagbar werden. Die unabdingbare
Voraussetzung für das Auftreten von deterministischem Chaos ist die
Nichtlinearität des untersuchten Systems. Die linearisierte Pendelgleichung,
bei der der Ausdruck sinq durch q ersetzt wird, zeigt kein chaotisches Verhalten. Mathematisch
gesprochen können alle nichtlinearen dynamischen Systeme mit mehr als zwei
Freiheitsgraden, insbesondere viele biologische, meteorologische oder
ökonomische Systeme, chaotisches Verhalten zeigen und damit über lange
Zeiträume unvorhersagbar werden. Die Tabelle zeigt, dass diese empfindliche
Abängigkeit von den Anfangsbedingung eine typische Eigenschaft zahlreicher
nichtlinearer Systeme ist.
Chaos 1: Chaotische Syteme. Bei konservativen Systemen bleibt die Energie erhalten, bei dissipativen Systemen, wie dem getriebenen Pendel, muss die dissipierte (z.B. durch Reibung verlorene) Energie durch Antrieb wieder von aussen zugeführt werden.
|
Chaotische
Systeme |
|
|
|
|
|
Dissipative Systeme |
Konservative Systeme |
|
Getriebenes Pendel |
Die meisten Systeme der klassischen Mechanik |
|
Flüssigkeiten bei einsetzender Turbulenz |
Planetenbewegung |
|
Laser |
Teilchenbeschleuniger |
|
Chemische Reaktionen |
|
Die Bernoulli-Abbildung
Um zu verstehen, wie
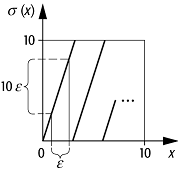
deterministisches Chaos zustande kommt, betrachten wir die in [3]Abb. 2 dargestellte iterative
Bernoulli-Abbildung ![]() ("t" bzw. "t +
1" sind hier nicht als Exponent, sondern als Iterations-Indizes
aufzufassen), die eine chaotische Punktfolge erzeugt. Diese Abbildung hat zwei
wesentliche Eigenschaften: Erstens verstärken sich kleine Fehler in den
Anfangsbedingungen (s.o.). Zweitens wird die Trajektorie - analog zur
Winkelvariablen beim Pendel - immer wieder auf ein endliches Intervall
zurückgefaltet. Die Differenz zwischen zwei Anfangswerten, die sich um e0 unterscheiden, wird schon nach einem Iterationsschritt
um einen Faktor 10 erhöht. Die Fehlerverstärkung erfolgt exponentiell mit der
Zeit t:
("t" bzw. "t +
1" sind hier nicht als Exponent, sondern als Iterations-Indizes
aufzufassen), die eine chaotische Punktfolge erzeugt. Diese Abbildung hat zwei
wesentliche Eigenschaften: Erstens verstärken sich kleine Fehler in den
Anfangsbedingungen (s.o.). Zweitens wird die Trajektorie - analog zur
Winkelvariablen beim Pendel - immer wieder auf ein endliches Intervall
zurückgefaltet. Die Differenz zwischen zwei Anfangswerten, die sich um e0 unterscheiden, wird schon nach einem Iterationsschritt
um einen Faktor 10 erhöht. Die Fehlerverstärkung erfolgt exponentiell mit der
Zeit t: ![]() . Der
Ljapunow-Exponent l
beschreibt dabei die Rate der exponentiellen Fehlerverstärkung und hat in
unserem Beispiel den Wert ln 10. Betrachten wir die Wirkung von s(x) z.B. auf den Anfangswert
. Der
Ljapunow-Exponent l
beschreibt dabei die Rate der exponentiellen Fehlerverstärkung und hat in
unserem Beispiel den Wert ln 10. Betrachten wir die Wirkung von s(x) z.B. auf den Anfangswert ![]() :
:

Wir sehen, dass die
Ziffern bei jeder Iteration um eine Stelle nach links wandern und alle Stellen
vor dem Komma, bis auf eine, abgeschnitten werden. Damit werden Ziffern, die in
p
weit hinter dem Komma stehen, eine nach der anderen nach vorne geholt und
"sichtbar gemacht". Stellen wir uns nun vor, dass die Anfangsbedingung
eine Zahl ist, die wir aus einem Experiment nur bis auf drei Stellen nach dem
Komma genau kennen, so können wir schreiben: ![]() , wobei die
Fragezeichen für die unbekannten Ziffern stehen. Nach drei bzw. vier
Iterationen mit s(x) erhalten wir
, wobei die
Fragezeichen für die unbekannten Ziffern stehen. Nach drei bzw. vier
Iterationen mit s(x) erhalten wir ![]() und
und ![]() , d.h. schon
die vierte Iterierte besteht nur noch aus Fragezeichen, ist also völlig
unbekannt. Wir können über sie somit keine Vorhersagen mehr machen, das System
zeigt chaotisches Verhalten. Wir sehen aber auch, dass für kurze Zeiten (im
obigen Beispiel für drei Zeitschritte) das Verhalten des chaotischen Systems
berechnet, d.h. vorhergesagt werden kann. Für längere Zeiten sind nur noch
statistische Aussagen über das Systemverhalten möglich.
, d.h. schon
die vierte Iterierte besteht nur noch aus Fragezeichen, ist also völlig
unbekannt. Wir können über sie somit keine Vorhersagen mehr machen, das System
zeigt chaotisches Verhalten. Wir sehen aber auch, dass für kurze Zeiten (im
obigen Beispiel für drei Zeitschritte) das Verhalten des chaotischen Systems
berechnet, d.h. vorhergesagt werden kann. Für längere Zeiten sind nur noch
statistische Aussagen über das Systemverhalten möglich.
Dissipative Systeme: Seltsame Attraktoren
Dies führt zum Begriff
des Seltsamen Attraktors. Nichtlineare Systeme lassen sich mit
Differentialgleichungen erster Ordnung von der Form ![]() mit
mit ![]() oder durch Iterationsgleichungen der Form
oder durch Iterationsgleichungen der Form ![]() beschreiben. Die Gesamtheit der Vektoren
beschreiben. Die Gesamtheit der Vektoren ![]() spannt den Phasenraum auf. Ein Attraktor ist
nun ein beschränktes Gebiet dieses Phasenraumes, in das die Trajektorie
spannt den Phasenraum auf. Ein Attraktor ist
nun ein beschränktes Gebiet dieses Phasenraumes, in das die Trajektorie ![]() im Laufe der Zeit gezogen wird. Einfache
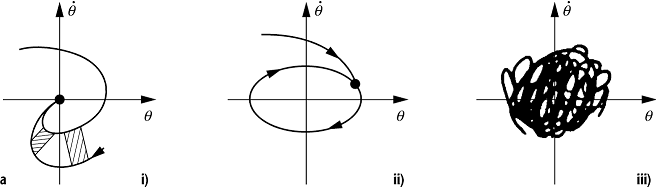
Attraktoren sind z.B. Fixpunkte
im Laufe der Zeit gezogen wird. Einfache
Attraktoren sind z.B. Fixpunkte
oder Grenzzyklen ([4]Abb. 3a, [5]Abb.
3b, [6]Abb.
3c, [7]Abb.
3d, [8]Abb.
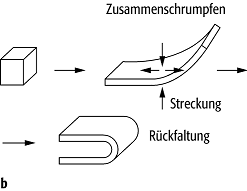
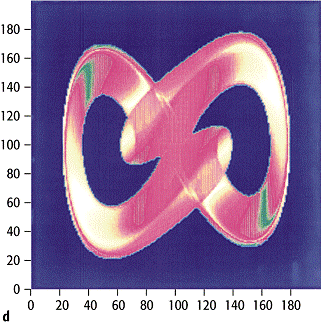
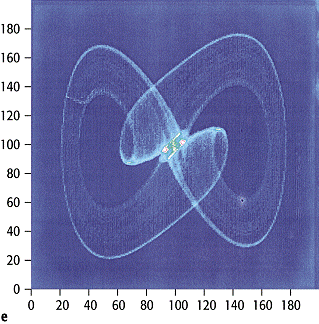
3e,). Ein Seltsamer Attraktor ist dadurch gekennzeichnet, dass in einem
beschränkten Gebiet des Phasenraumes benachbarte Punkte im Laufe der Zeit
exponentiell auseinanderlaufen. [9]Abb.
3b und [10]Abb.
3c zeigen, wie in einem dissipativen System, in welchem die Energie nicht
erhalten ist, sondern z.B. durch Reibung dissipiert wird, Chaos entsteht: durch
Strecken und Falten entsteht aus einem Würfel im Phasenraum unter dem Einfluss
der chaotischen Dynamik eine fraktale Blätterteigstruktur, die die
Eigenschaften eines Seltsamen Attraktors besitzt ([11]Abb.
3b). Der in [12]Abb.
3c gezeigte Poincaré-Schnitt dieses Attraktors zeigt diese Struktur ebenfalls.
Kenngrössen des Attraktors sind einmal seine Punktdichte r(![]() ) - sie gibt
an, wie häufig ein Punkt des Phasenraums von der Trajektorien besucht wird -
und zum anderen seine lokalen Ljapunow-Exponenten
) - sie gibt
an, wie häufig ein Punkt des Phasenraums von der Trajektorien besucht wird -
und zum anderen seine lokalen Ljapunow-Exponenten ![]() , die angeben,
wie rasch benachbarte Trajektorien in unterschiedliche Richtungen lokal
separieren ([13]Abb.
3d und [14]Abb.
3e).
, die angeben,
wie rasch benachbarte Trajektorien in unterschiedliche Richtungen lokal
separieren ([13]Abb.
3d und [14]Abb.
3e).
Wege ins Chaos
Ein wichtiges Ziel der
Chaosforschung ist es, das Einsetzen von Turbulenz zu verstehen. Während aber
Turbulenz in realen Flüssigkeiten oder Gasen ein raum-zeitliches Phänomen ist,
d.h. viele Freiheitsgrade betrifft, hat man bisher nur Übergänge ins rein
zeitliche deterministische Chaos mit wenigen Freiheitsgraden untersucht. Ein
wichtiger Weg ins zeitliche Chaos ist die sogenannte Periodenverdopplungsroute
oder Feigenbaumroute. Sie wurde von Grossmann und Thomae (1977) und von M.J.
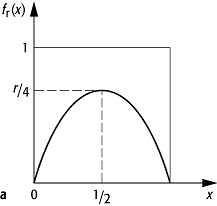
Feigenbaum (1978) durch Untersuchung der logistischen Abbildung ![]() gefunden. Diese Abbildung beschreibt z.B. das
Wachstum einer Tierpopulation auf einer beschränkten Fläche, wobei xt die auf das
Intervall [0, 1] normierte Individuenzahl der Population ist. Diese Abbildung
führt für komplexe Werte von r und xt zu den fraktalen
Formen der Mandelbrot-Mengen (der sog. Apfelmännchen). Kleine Populationen mit
gefunden. Diese Abbildung beschreibt z.B. das
Wachstum einer Tierpopulation auf einer beschränkten Fläche, wobei xt die auf das
Intervall [0, 1] normierte Individuenzahl der Population ist. Diese Abbildung
führt für komplexe Werte von r und xt zu den fraktalen
Formen der Mandelbrot-Mengen (der sog. Apfelmännchen). Kleine Populationen mit ![]() wachsen exponentiell, denn dann ist
wachsen exponentiell, denn dann ist ![]() und damit
und damit ![]() . Für grosse xt wird das Wachstum
durch den beschränkten Futtervorrat auf der Fläche, d.h. den Faktor (1 - xt), gebremst. Wenn
man die Iterierten x1,
x2, ...
der logistischen Abbildung mit dem Computer für verschiedene Werte des
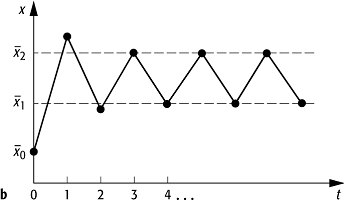
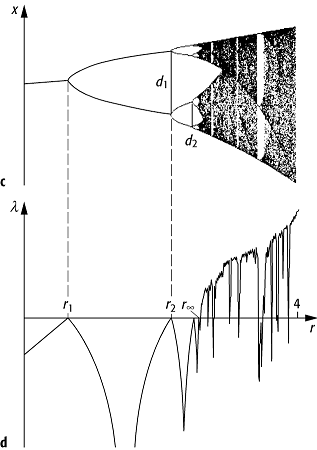
Kontrollparameters r berechnet, so erhält man [15]Abb. 4b. Für kleine Werte des
Kontrollparameters hat die Abbildung einen Fixpunkt. Dieser wird bei r =
r1 instabil zugunsten eines Zweierzyklus, bei r = r2
entsteht ein Viererzyklus, bei r = rn ein Zyklus der
Länge 2n. Schliesslich wird bei einem endlichen Wert r ¥
=
3,5699456... die Zykluslänge unendlich. Die normierte Individuenzahl xt
der Population springt zwischen unendlich vielen Werten hin und her, das System
fängt an, Chaos zu zeigen, und der Ljapunow-Exponent l wird bei r ¥ positiv.
Feigenbaum hat als erster erkannt, dass diese Periodenverdopplungsroute ins
Chaos universelle Eigenschaften hat. Sie tritt für alle Abbildungen auf, die im
Einheitsintervall nur ein quadratisches Maximum haben, z.B. auch für
. Für grosse xt wird das Wachstum
durch den beschränkten Futtervorrat auf der Fläche, d.h. den Faktor (1 - xt), gebremst. Wenn
man die Iterierten x1,
x2, ...
der logistischen Abbildung mit dem Computer für verschiedene Werte des
Kontrollparameters r berechnet, so erhält man [15]Abb. 4b. Für kleine Werte des
Kontrollparameters hat die Abbildung einen Fixpunkt. Dieser wird bei r =
r1 instabil zugunsten eines Zweierzyklus, bei r = r2
entsteht ein Viererzyklus, bei r = rn ein Zyklus der
Länge 2n. Schliesslich wird bei einem endlichen Wert r ¥
=
3,5699456... die Zykluslänge unendlich. Die normierte Individuenzahl xt
der Population springt zwischen unendlich vielen Werten hin und her, das System
fängt an, Chaos zu zeigen, und der Ljapunow-Exponent l wird bei r ¥ positiv.
Feigenbaum hat als erster erkannt, dass diese Periodenverdopplungsroute ins
Chaos universelle Eigenschaften hat. Sie tritt für alle Abbildungen auf, die im
Einheitsintervall nur ein quadratisches Maximum haben, z.B. auch für ![]() . Das
Verhältnis
. Das
Verhältnis ![]() strebt für n
strebt für n ![]() ¥
gegen den Wert d
= 4,6692016, das Verhältnis
¥
gegen den Wert d
= 4,6692016, das Verhältnis ![]() (dn beschreibt im
wesentlichen den Abstand benachbarter Fixpunkte, siehe [16]Abb.
4c) gegen den Wert a
= 2,5029078. a
und d werden als die universellen
Feigenbaum-Zahlen bezeichnet. Diese universellen Werte lassen sich im Rahmen
der Renormierungsgruppentheorie verstehen. Die Periodenverdopplungsroute und
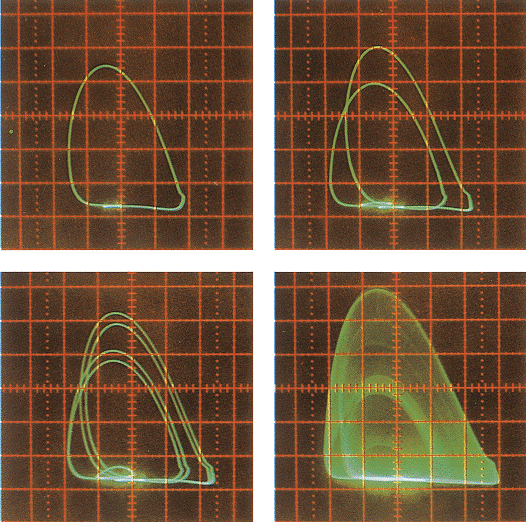
mit ihr die Feigenbaumzahlen wurden in vielen Systemen experimentell gefunden ([17]Abb.
5). Ausser der Feigenbaumroute gibt es noch eine Fülle anderer Wege ins Chaos,
die ebenfalls universelles Verhalten zeigen.
(dn beschreibt im
wesentlichen den Abstand benachbarter Fixpunkte, siehe [16]Abb.
4c) gegen den Wert a
= 2,5029078. a
und d werden als die universellen
Feigenbaum-Zahlen bezeichnet. Diese universellen Werte lassen sich im Rahmen
der Renormierungsgruppentheorie verstehen. Die Periodenverdopplungsroute und
mit ihr die Feigenbaumzahlen wurden in vielen Systemen experimentell gefunden ([17]Abb.
5). Ausser der Feigenbaumroute gibt es noch eine Fülle anderer Wege ins Chaos,
die ebenfalls universelles Verhalten zeigen.
Konservative Systeme: das KAM-Theorem
Wir kommen nun zum
zweiten Zweig der Tabelle, der die Bewegung in konservativen Systemen
beschreibt. Schon 1893 wusste der französische Mathematiker H. Poincaré, dass die
Bewegungsgleichungen von drei durch Gravitation wechselwirkenden Körpern
(Dreikörperproblem) nicht integrabel sind und zu völlig chaotischen Bewegungen
im Raum führen können. Das Studium konservativer (d.h. nicht-dissipativer)
chaotischer Systeme wird dadurch erschwert, dass es aus Gründen der
Energieerhaltung keine Attraktoren wie bei dissipativen Systemen gibt. Um 1950
bewiesen A.N. Kolmogorow, W.I. Arnold und J. Moser das sogenannte
Kolmogorow-Arnold-Moser-Theorem (KAM-Theorem). Es besagt, dass die Bewegung im
Phasenraum der klassischen Mechanik weder vollständig regulär noch vollständig
chaotisch ist, sondern dass das Verhalten der Trajektorie empfindlich von den
Anfangsbedingungen abhängt. Das bedeutet, dass stabile, reguläre Bewegung, wie
sie in den meisten Lehrbüchern behandelt wird, bei klassischen Systemen die
Ausnahme ist! Abb. 6 zeigt die sog. Cassinische Teilung im Ring des Saturn. Sie
ist darauf zurückzuführen, dass die Trajektorien im Gebiet der Cassinischen
Teilung instabil sind, so dass die Gesteinsbrocken, die sich bei der Entstehung
des Saturnringes zunächst dort befanden, im Laufe der Zeit chaotisch
abgewandert sind.
Ausblick
Das Langzeitverhalten
konservativer chaotischer Systeme berührt eine ganze Reihe grundsätzlicher
Fragen, die von der Stabilität des Sonnensystems über die Stabilität von
Strahlen in Teilchenbeschleunigern bis hin zur Begründung der Ergodenhypothese
der statistischen Mechanik reichen. Zu den wichtigsten neuen Zweigen der
Chaosforschung gehören die Erforschung des Quantenchaos, wo die Frage untersucht
wird, wie sich quantenmechanische Systeme verhalten, deren klassischer
Grenzfall Chaos zeigt, und das Phänomen der Chaoskontrolle, bei dem durch
Rückkopplung in chaotischen Systemen ursprünglich instabile Trajektorien
resonanzartig stabilisiert werden. Die wesentliche Grunderkenntnis aus der
Entdeckung des deterministischen Chaos in dissipativen und konservativen
Systemen ist die, dass selbst schon recht einfache Systeme in ihrem
Langzeitverhalten unvorhersagbar werden. Diese Einsicht wird uns bei der
täglichen Wettervorhersage zwar vor Augen geführt, sie wurde uns aber erst
durch die Entdeckung des deterministischen Chaos in ihren Wurzeln verständlich.
Chaos 1: Das
getriebene Pendel: a) Sein Winkel q verhält sich als Funktion der Zeit t chaotisch.
b) Zwei Trajektorien im Phasenraum (q, ![]() ), die sich
durch die Anfangsbedingungen unterscheiden, laufen mit der Zeit exponentiell
auseinander (grau: q(t
= 0) = 0,
), die sich
durch die Anfangsbedingungen unterscheiden, laufen mit der Zeit exponentiell
auseinander (grau: q(t
= 0) = 0, ![]() (t = 0)
= 0, schwarz: q(t
= 0) = 0,
(t = 0)
= 0, schwarz: q(t
= 0) = 0, ![]() (t = 0)
= 0,2). Die Bahnen wurden durch numerische Integration der Pendelgleichung
(t = 0)
= 0,2). Die Bahnen wurden durch numerische Integration der Pendelgleichung ![]() erhalten mit den Werten g = 0,3 für die Dämpfungskonstante, A
= 4,5 für das Antriebsmoment und w = 0,6 für die Antriebsfrequenz.
erhalten mit den Werten g = 0,3 für die Dämpfungskonstante, A
= 4,5 für das Antriebsmoment und w = 0,6 für die Antriebsfrequenz.
Chaos 2: Die
Bernoulli-Abbildung ![]() .
.
Chaos 3: Seltsame Attraktoren: a) schematische Darstellung verschiedener Attraktoren im Phasenraum des getriebenen Pendels: (i) Fixpunkt, (ii) Grenzzyklus, (iii) Seltsamer Attraktor; b) durch Streckung und Faltung entsteht aus einem Würfel eine fraktale "Blätterteigstruktur"; der Poincaré-Schnitt des zum Duffing-Oszillator gehörenden Seltsamen Attraktors (c) zeigt ebenfalls diese Struktur. Auf diesem Attraktor, der eine schleifenförmige Struktur besitzt, sind die lokalen Ljapunow-Exponenten l (d) ganz anders verteilt als die lokalen Punktdichte r; e) Eine hohe lokale Instabilität, d.h. ein grosser lokaler Ljapunow-Exponent, geht also durchaus nicht in Hand mit einer besonders hohen oder niedrigen lokalen Aufenthaltswahrscheinlichkeit. Die Farbskala reicht für beide Variablen von blau (minimal) bis gelb (maximal).
Chaos 4: Die Periodenverdopplungsroute ins Chaos: a) die logistische Abbildung, b) ein Zweierzyklus stellt sich ein. c) Die Iterierten der logistischen Abbildung als Funktion des Kontrollparameters r zeigen den Übergang von einfacher über doppelte und vierfache Periode ins Chaos (unendlich grosse Periode). d) Der Liapunov-Exponent der logistischen Abbildung als Funktion des Kontrollparameters r; er ist für r < r ¥ negativ oder Null (Dämpfung) und kann oberhalb von r ¥ positive Werte annehmen (exponentielle Verstärkung).
b
Chaos 5: Die Periodenverdopplungsroute bei einem nichtlinearen elektronischen Oszillator. a) Der getriebene Schwingkreis enthält eine nichtlineare Kapazitätsdiode C; b) Die Oszilloskopbilder zeigen die Strom-Spannungs-Kennlinie für verschiedene Werte der Antriebsspannung V0. Man erkennt den Übergang von einfacher über doppelte und vierfache Periode ins Chaos (unendlich grosse Periode).
bottom:.0001pt;border:none; mso-border-left-alt:solid purple 1.5pt;mso-border-bottom-alt:solid purple 1.5pt; mso-border-right-alt:solid purple 1.5pt;padding:0cm;mso-padding-alt:0cm 13.0pt 13.0pt 13.0pt\'>Chaos 6: Die Cassinische Teilung. Der Ring des Saturn (links) zeigt eine grosse Lücke, die sog. Cassinische Teilung (rechts), da die Bewegung auf Bahnen in diesem Raumgebiet instabil ist.
Techniklexikon.net
Das freie Technik-Lexikon. Fundierte Informationen zu allen Fachgebieten der Ingenieurwissenschaften, für Wissenschaftler, Studenten, Praktiker & alle Interessierten. Professionell dargeboten und kostenlos zugängig.
Techniklexikon
Modernes Studium der Physik sollte allen zugängig gemacht werden.