Techniklexikon

Bessel-Funktionen

Zylinderfunktionen, ein Satz spezieller mathematischer Funktionen. Die Bessel-Funktion m-ter Ordnung wird mit J_m(x) bezeichnet, wobei m ganzzahlig ist. Bessel-Funktionen sind Lösungen der Bessel-Gleichung. Sie können auch über ihre erzeugende Funktion  definiert werden, in deren Laurent-Reihenentwicklung  sie als Koeffizienten auftreten. Weitere mögliche Definitionen sind die Integraldarstellung  und die Reihenentwicklung

.

Bessel-Funktionen oszillieren mit einer Amplitude, die für x   ¥  wie x ^{- 1/2} abklingt. Sie dürfen nicht mit den sphärischen Bessel-Funktionen j_n(x) verwechselt werden, welche die sphärische Bessel-Gleichung lösen, ebenfalls oszillieren, aber wie x ^{- 1} abklingen. Bessel-Funktionen spielen z.B. in der Theorie der Beugung oder bei der Diskussion zylindrischer Hohlraumresonatoren eine grosse Rolle.

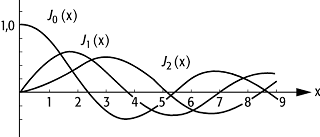
Bessel-Funktionen: Verlauf von J₀(x), J₁(x) und J₂(x).