Techniklexikon

begleitendes Dreibein

entlang der Raumkurve eines Massenpunktes mitbewegte rechtshändige Orthonormalbasis, deren Basisvektoren der Tangentenvektor, der Hauptnormalenvektor und der Binormalenvektor der Kurve sind.

Der Tangentenvektor t(t) ist der Einheitsvektor in Richtung der Tangente an die Bahn, der Hauptnormalenvektor h(t) liegt gleichfalls in der momentanen Bahnebene, steht aber senkrecht zum Tangentenvektor, und der Binormalenvektor b(t) steht senkrecht auf der momentanen Bahnebene. Diese drei Einheitsvektoren bilden zusammen ein Rechtssystem.

Den Zusammenhang zwischen der Raumkurve bzw. ihrer Parametrisierung r(t) und den obigen drei Normalenvektoren liefern die Frenetschen Formeln

,  und .

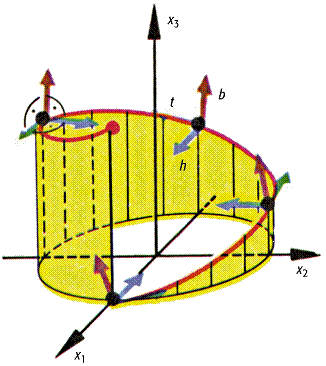
begleitendes Dreibein: Beim Durchlaufen der Bahn mitbewegtes Bezugssystem.