Bandstruktur

Energiebandstruktur. Darstellung der quanti tatixen Energieabhängigkeit der freien Elektronen bzw. Defektelektronen im (reziproken) Gitter eines r Halbleiters. Anders als beim Bändermodell werden in der B. die erlaubten und verbotenen Energiebänder in ihrer komplizierten Abhängigkeit vom Kristallgitter dargestellt, wobei nicht die direkte Ortsabhängigkeit (Gittervektor a), sondern deren Reziprokwert zugrunde gelegt wird; dieser entspricht dem quantenmechanischen Impuls der Elektronen k. Die Energieachse verläuft dabei durch den Impulswert k= 0. Wie aus der B. ersichtlich, besteht in Wirklichkeit jedes Energieband aus einzelnen Teilbändern mit Maxima und Minima. Von besonderer Bedeutung für die Emission von Strahlung ist der in der Zonenmitte gelegene Bandübergang. Die B. ist zur Charakterisierung eines Halbleiters außerordentlich wichtig, da sich daraus zahlreiche Eigenschaften wie Ladungsträgerbeweglichkeit, energetische Verteilung der Ladungsträger, Bandabstand £g usw., aber auch der Verlauf grundlegender Elementarprozesse ableiten lassen. Das Bändermodell wird durch die B. begründet und stellt eine starke Vereinfachung der Halbleiter-B. dar. das Energiespektrum der Elektronen im idealen Kristall. Es kann vor allem bei Halbleitern und Isolatoren durch Störstellen wesentlich beeinflusst werden. Die elektronische Struktur eines Materials ist eine Schlüsselgrösse für die theoretische Beschreibung der Eigenschaften des Festkörpers.

Da ein Festkörper ein Vielteilchensystem von grössenordnungsmässig 10²⁴ Teilchen/cm³ ist, kann die Wellenfunktion aller Elektronen nicht mehr berechnet werden. Man kann aber die Bewegung eines einzelnen Elektrons angenähert beschreiben, indem man ein gemitteltes Potential annimmt, bei dem das periodische Potential der Atomrümpfe und der anderen Elektronen berücksichtigt werden. 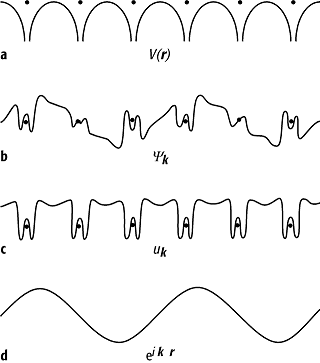Gemäss dem Bloch-Theorem kann die Wellenfunktion eines Elektrons im periodischen Kristallpotential durch eine Bloch-Welle  beschrieben werden, das ist eine ebene Welle e^iKr, die durch eine periodische Funktion, die Bloch-Funktion u_K(r), moduliert ist (Abb. 1), wobei K der Wellenzahlvektor ist.

Die Periodizität des Gitters führt zur Ausbildung von erlaubten und verbotenen Energiebereichen, den Energiebändern und Energielücken. Anschaulich kann man die Entstehung dieser Bandstruktur so verstehen:

Die Energie des freien Elektrons als Funktion des Wellenzahlvektors ist eine Parabel  und kann einen beliebigen Wert annehmen. In einem Kristall besteht jedoch der Zusammenhang E(K) ~ K² nicht, sondern es treten Unstetigkeiten an den Stellen K ~ np auf, wobei n = 1, 2, 3, ... der sog. Bandindex ist. Diese Unstetigkeiten lassen sich anschaulich so verstehen, dass Bragg-Reflexion an den Rändern der Brillouin-Zonen stattfindet, so dass sich stehende Wellen ausbilden, bei denen die Dichte der Elektronen an den positiven Atomrümpfen entweder überhöht oder erniedrigt ist, wobei die Erhöhung der Dichte energetisch günstiger ist als die Erniedrigung. Dadurch wird die Energieparabel am Rand einer Brillouin-Zone aufgespalten, und es entsteht an dieser Stelle eine Energielücke (Bandlücke), die um so breiter ist, je grösser der Einfluss des Kristallpotentials ist.

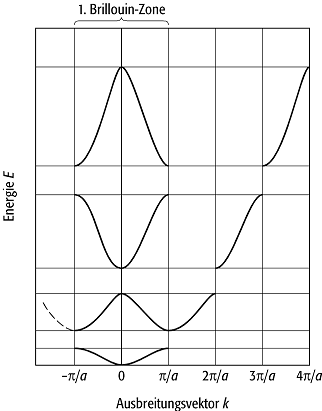
Zur graphischen Verdeutlichung der Bandstruktur trägt man üblicherweise E(K) über einer bestimmten K-Richtung (Abb. 2) auf. Dabei stellt man über der ersten Brillouin-Zone das tiefste Valenzband, über der zweiten Brillouin-Zone das nächste Band usw. dar. Dies führt zum sog. ausgebreitetenen Zonenschema.

Es lässt sich nun zeigen, dass man zur vollständigen Charakterisierung der Energiezustände (man spricht auch von den Bloch-Zuständen) die Wellenzahlvektoren auf die erste Brillouin-Zone beschränken kann. Sei k der Wellenzahlvektor in der ersten Brillouin-Zone und K allgemein ein Vektor ausserhalb dieser Zone, so gibt es wegen der Translationssymmetrie des reziproken Gitters immer einen reziproken Gittervektor l g (l = 0,  ± 1,  ± 2, ...), der K auf die erste Brillouin-Zone reduziert, d.h. dem Vektor K durch Addition einen Vektor k im Innern der ersten Brillouin-Zone zuordnet:

k = K  -  l g, K = k + l g.

k heisst der reduzierte Wellenzahlvektor zum freien Wellenzahlvektor K. Die Reduktion aller Vektoren K bedeutet geometrisch die Verschiebung der höheren Brillouin-Zonen über die erste Brillouin-Zone (vgl. Abb. 2). Das sich ergebende Schema wird reduziertes Zonenschema genannt. Die Energie E(K) lässt sich dann als Funktion des reduzierten Wellenzahlvektors und des Bandindex n angeben, also als E_n(k), wobei der Bandindex n eine ganzzahlige Laufnummer ist (n = 1,2,...) und über n/2 =  ± l mit dem oben eingeführten Parameter l zusammenhängt. Zusammenfassend kann gesagt werden, dass der Wellenzahlvektor eines Bloch-Zustandes nur bis auf Vielfache des reziproken Gittervektors definiert ist, d.h. alle Wellenzahlvektoren K = k(mod g) sind in diesem Sinne äquivalent. Durch die Reduktion aller dieser Vektoren auf einen Repräsentanten in der ersten Brillouin-Zone wird eine eindeutige Angabe des Wellenzahlvektors und der Bloch-Zustände erreicht. Darin liegt die wesentliche Bedeutung der Reduktion.

Geht man umgekehrt vom reduzierten Zonenschema aus und transformiert innerhalb der einzelnen Bänder von den reduzierten Wellenzahlvektoren k auf beliebige äquivalente Wellenzahlvektoren k ¢  = k + l ¢ g, so entsteht quasi durch "Mitnahme der Energien" das sog. periodisch wiederholte Zonenschema.

Zur Berechnung der Bandstruktur existieren unterschiedliche Methoden, die möglichst selbstkonsistente Rechnungen sein sollten. Um zu viele Näherungen und hohen Rechenaufwand zu vermeiden, nutzt man oft empirische Methoden, z.B. die empirische Pseudopotentialmethode, die die Bandstruktur an experimentelle Daten anpasst. Schliesslich sind Methoden entwickelt worden, die von einem gewählten Kristallpotential ausgehen und die Schrödinger-Gleichung mit diesem nunmehr bekannten Potential lösen (OPW-Methode, LCAO-Methode, APW-Methode, KKR-Methode, Atomorbital). Diese zuletzt genannten Methoden sind vorwiegend für Metalle benutzt worden. Um den numerischen Rechenaufwand zu verringern, werden bei den Rechnungen die Symmetrieeigenschaften der Bloch-Funktionen weitgehend ausgenutzt.

Die Bandstruktur beschreibt nur das Einelektronenspektrum des Festkörpers. Mehrteilchenanregungen, wie Exzitonen und Plasmonen, sind in diesem Modell nicht enthalten. In moderner Auffassung erfasst die Bandstruktur aber weit mehr als das Energiespektrum in einem Modell unabhängiger Elektronen, sie ist also insbesondere nicht an die Konzeption des Hartree- bzw. Hartree-Fock-Verfahrens gebunden. Das von Landau entwickelte Konzept der Quasiteilchen erlaubt, das Einelektronenspektrum als Spektrum entsprechender Elementaranregungen des elektronischen Vielteilchensystems zu interpretieren und liefert so eine theoretische Basis für den Erfolg des Einelektronenkonzepts. Der Formalismus der Dichtefunktionaltheorie vertieft die theoretische Basis für die Berechnung der Bandstruktur, insbesondere führt er auf ein Kristallpotential, bei dessen Konstruktion die von der elektrostatischen Abstossung des Elektrons bewirkten Korrelationseffekte berücksichtigt werden.

Bandstruktur 1: a) Schematische Darstellung des Kristallpotentials V(r); b) Die Wellenfunktion Y_k(r) für das Elektron (Bloch-Welle) setzt sich aus zwei Anteilen zusammen, einem Anteil c), der mit dem Gitter periodisch ist, dem Bloch-Faktor u_k(r), und d) einer ebenen Welle e^ikr.

Bandstruktur 2: Energiebänder in ausgebreitetem und reduziertem Zonenschema.