Atom- und Ionenfallen

Petra Nordinghaus-Martin
Die Atomphysiker haben eine Reihe verschiedener Methoden ersonnen, mit denen sie Atome auf eng begrenztem Raum halten oder "einfangen" können. Wenn es gelingt, die Atome über längere Zeiträume einzuschliessen, kann ihre innere Struktur mit extrem hoher Genauigkeit gemessen werden. Diese Möglichkeit ist deshalb von Interesse, weil auf diese Weise die Theorien über den Atombau sorgfältig überprüft werden können. Wie immer, wenn zwischen theoretischer Vorhersage und experimentellen Resultaten eine Abweichung auftritt - und sei sie noch so klein -, muss die Theorie modifiziert werden. Von höchster Bedeutung sind dabei die Fälle, bei denen zur Erklärung von Abweichungen ein neuer physikalischer Effekt eingeführt werden muss, der nachfolgend in die Theorie zu integrieren ist.
Ein anderes Motiv für
den Einfang von Atomen liegt in der Physik begründet, die sich mit der
Beschreibung der eingeschlossenen Atome beschäftigt, und die selbst recht
interessant sein kann. Das gilt vor allem bei tiefen Temperaturen, bei der die
quantenmechanische Natur der Bewegung der Atome in den Fallen deutlich wird.
Beispiele hierfür sind die Untersuchung atomarer Stösse bei so geringen
Geschwindigkeiten, dass die De-Broglie-Wellenlänge des Atoms gross gegenüber dem
Wechselwirkungsabstand ist, und die Erzeugung und Untersuchung verschiedener
nichtklassischer Bewegungszustände in der Falle. Bei tiefen Temperaturen
spielen auch kollektive Effekte eine wichtige Rolle. Beispielsweise kann eine
Akkumulation eingeschlossener, ionisierter Atome als ein
"Einkomponenten-Plasma" angesehen werden. Werden die Ionen gekühlt,
so zwingt das Gleichgewicht zwischen den Feldern, die den Einschluss bewirken,
und der Coulomb-Abstossung zwischen den Ionen letztere dazu, in kristalliner
Form zu kondensieren ([27]Abb. 3 neutraler Atome gekühlt, so
zeigen die Atome aufgrund ihrer relativ schwachen Wechselwirkung ein der
Quantenstatistik gehorchendes Verhalten. Bosonische Atome bei hoher Dichte und
tiefer Temperatur sind daher ein System, an dem die Bose-Einstein-Kondensation
eines Gases beobachtet werden kann, ein Phänomenen, das in gewisser Weise ein
Analogon zur Suprafluidität in Flüssigkeiten und zur Supraleitung in
Festkörpern darstellt. Die tiefen Temperaturen, die die Voraussetzung solcher
Experimente sind, erreicht man mit Hilfe von Laserkühlung. Diese kann auf
verschiedene Weise realisiert werden, und man erreicht extrem tiefe
Temperaturen ( < 1 mK);
dabei werden die Atome bis auf den quantenmechanischen Grundzustand der
Bewegung abgekühlt.
Ein Typ der
Atomfallen, der sowohl auf geladene als auch auf neutrale Atome anwendbar ist,
beruht auf "ponderomotorischen" Kräften, auf Kräften also, die von
einem elektromagnetischen Feld auf eine Ladung ausgeübt werden und die zu einer
Verschiebung der mit dieser Ladung verbundenen Masse führen. Die prinzipielle
Wirkungsweise dieser Fallen kann man sich an folgendem eindimensionalen
Beispiel klar machen. Nehmen wir an, ein leichtes, geladenes Teilchen sei über
eine Feder mit einem viel schwereren Teilchen verbunden ([28]Abb. 1). Die Teilchen können sich in
horizontaler Richtung frei bewegen, so dass die Bewegung im wesentlichen zwei
Komponenten hat: eine gleichförmige Translation des Schwerpunkts der beiden
Teilchen sowie eine Streckschwingung der beiden Teilchen mit einer Frequenz n0, die von den Massen und von der Federkonstanten
abhängt. Weil wir voraussetzten, dass die Masse des einen Teilchens viel kleiner
als die des anderen ist, wird die Streckschwingung durch die Bewegung der
kleineren Masse bestimmt. Nun wirke in horizontaler Richtung ein räumlich
gleichförmiges elektrisches Feld ein, das mit der Frequenz n oszilliert. Dieses Feld regt vor
allem die leichte Masse zu einer Schwingung mit der Frequenz n an. Die über eine Schwingungsdauer (
= 1/n) gemittelte Kraftwirkung des
elektrischen Feldes ist null. Das gleiche gilt für die schwerere Masse. Für n > n0 ist die Bewegung des leichten Teilchens relativ zum elektrischen
Feld phasenverschoben; für n < n0 hingegen ist seine Bewegung mit dem Feld in Phase.
Jetzt nehmen wir an, in dem Feld werden leichte Inhomogenitäten erzeugt. Mit
"leicht" meinen wir dabei, dass die Änderung der Feldamplitude über
die gesamte Bewegung des leichten Teilchens bei der Frequenz n nur einen kleinen Bruchteil der
gesamten Feldamplitude ausmacht. In diesem Fall ist die Kraft auf die zwei
Teilchen im Mittel nicht null, sondern wird durch die Kraft auf das leichte
Teilchen bestimmt. Für n
> n0 wirkt diese mittlere Kraft in Richtung des Gebietes
geringerer elektrischer Feldstärke. Zur Verdeutlichung nehmen wir an, das
elektrische Feld sei in [29]Abb.
1 nach rechts hin stärker. Wenn die Kraft nach rechts wirkt, wird das Teilchen
nach links ausgelenkt, und umgekehrt. Im letztgenannten Fall ist die auf das
leichte Teilchen einwirkende Feldstärke jedoch höher. Die resultierende Wirkung
besteht darin, dass die mittlere Kraft nach links wirkt, das heisst in Richtung
abnehmender Feldstärke. Umgekehrt wirkt für n < n0 die mittlere Kraft zum Gebiet höherer Feldstärke hin.
Betrachten wir nun den
Spezialfall n = n0. Hier fehlt die in [30]Abb. 1 gezeigte Feder, und wir
verfolgen nur die Bewegung des leichten, geladenen Teilchens. Die
ponderomotorische Kraft wirkt in Richtung abnehmender Feldstärke, denn es ist n > n0 = 0. In [31]Abb.
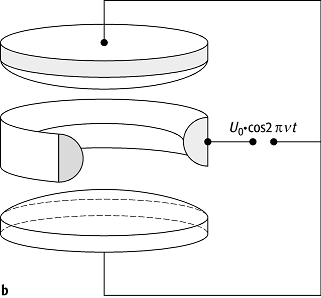
1b) wird die nach ihrem Erfinder W. Paul benannte Paul-Falle gezeigt, deren
Elektrodenanordnung (Quadrupol) bewirkt, dass die elektrische Feldstärke aus
allen Richtungen zur Fallenmitte hin kleiner wird. Mit dieser Konfiguration
kann man ionisierte Atome unabhängig vom Vorzeichen ihrer Ladung nahe der Mitte
zwischen den Elektroden einschliessen. Typische Parameter einer solchen
Ionenfalle sind U0 = 100 V und n0 = 1 MHz; der Elektrodenabstand liegt bei 1 cm ([32]Abb.
2).
Eine andere Form von Ionenfallen, bei der ponderomotorische Kräfte genutzt werden, sind die Speicherringe für hochenergetische Teilchen. Hier setzt man inhomogene statische Feldkonfigurationen ein. Im mitbewegten Bezugssystem der Teilchen, die diese Felder durchlaufen, wirken letztere wie oszillierende Felder, so dass auch hier eine Einschlusswirkung auftritt.
Der Fall n0 = 0 kann durch ein neutrales Atom realisiert werden, bei dem ein atomares Elektron (das leichte Teilchen) mit dem viel schwereren Atomkern verbunden ist. Hier liegt die Resonanzfrequenz n0 der "Coulomb-Feder" im sichtbaren Teil des Spektrums (5 × 1014 Hz). Mit Hilfe fokussierter Laserstrahlen mit besonderen räumlichen Mustern kann man ein lokales elektrisches Feldmaximum erzeugen, so dass sich bei n < n0 eine "rotverschobene optische Dipolfalle" um den Punkt maximaler Feldstärke bildet. Umgekehrt liegt bei n > n0 eine "blauverschobene optische Dipolfalle" vor, in der die Atome von einem Gebiet minimaler Feldstärke angezogen werden.
Führt man Ionen oder Atome in die Fallen, so kann die Amplitude ihrer Bewegung darin gross sein; das bedeutet, ihre Temperatur kann hoch sein. Um die Temperatur zu senken, verwendet man unterschiedliche Formen der Laserkühlung. Die Kühlwirkung resultiert aus dem mechanischen Impuls, der auf die Atome übertragen wird, wenn sie das Licht streuen. Bei geeigneter Frequenz des Laserstrahls und entsprechender räumlicher Anordnung kann man erreichen, dass die Atome das Licht nur dann streuen, wenn dadurch ihr Impuls verringert wird. Wir beschreiben hier die häufigste Art der Laserkühlung geladener oder neutraler Atome, nämlich die sogenannte Doppler-Kühlung.
Zunächst soll mit Hilfe eines durchstimmbaren Lasers das Absorptionsspektrum eines Atoms in der Nähe eines seiner optischen Übergänge vermessen werden. Könnten wir das Atom an einem festen Ort halten, wäre die Absorption bei einer bestimmten Frequenz n0 am stärksten, und es läge ein enger Frequenzbereich n vor (die natürliche Linienbreite), über den die Absorption sehr stark ist. Typische Werte sind n0 = 5 × 1014 Hz und n = 10 MHz.
Nun werde das Atom
freigelassen und einem Laserstrahl ausgesetzt, der von links auf das Atom
trifft. Dieser Laser habe die Frequenz nL, wobei nL < n0 ist. Wenn sich das Atom
mit der Geschwindigkeit ![]() nach links (also entgegengesetzt zum
Laserstrahl) bewegt, dann scheint in seinem Bezugssystem das Laserlicht
aufgrund des Doppler-Effekts eine Frequenz zu haben, die etwa bei nL(1 +
nach links (also entgegengesetzt zum
Laserstrahl) bewegt, dann scheint in seinem Bezugssystem das Laserlicht
aufgrund des Doppler-Effekts eine Frequenz zu haben, die etwa bei nL(1 + ![]() /c)
liegt. Bei einem bestimmten Wert von
/c)
liegt. Bei einem bestimmten Wert von ![]() ist nL(1 +
ist nL(1 + ![]() /c) = n0, und das Atom
absorbiert und reemittiert Photonen mit hoher Rate. Bei der Absorption wird der
Impuls des Photons auf das Atom übertragen, wobei dessen Impuls um h/l
reduziert wird (darin ist l die Wellenlänge des Lichts, und h ist
das Plancksche Wirkungsquantum). Jedoch läuft die Reemission der Photonen
räumlich symmetrisch ab; daher ändert sich durch die Reemission im Mittel der
Impuls des Atoms nicht. Bei jedem Streuvorgang wird also der Impuls des Atoms
im Mittel um h/l reduziert.
/c) = n0, und das Atom
absorbiert und reemittiert Photonen mit hoher Rate. Bei der Absorption wird der
Impuls des Photons auf das Atom übertragen, wobei dessen Impuls um h/l
reduziert wird (darin ist l die Wellenlänge des Lichts, und h ist
das Plancksche Wirkungsquantum). Jedoch läuft die Reemission der Photonen
räumlich symmetrisch ab; daher ändert sich durch die Reemission im Mittel der
Impuls des Atoms nicht. Bei jedem Streuvorgang wird also der Impuls des Atoms
im Mittel um h/l reduziert.
Wenn sich das Atom
statt dessen aber nach rechts (also in Richtung des Laserstrahls) bewegt,
erhöht jeder Streuvorgang seinen Impuls um h/l, die Streurate ist jetzt
jedoch geringer, weil die Frequenz der Strahlung im Bezugssystem des Atoms nun nL(1 - ![]() /c) < nL < n0 ist; der Laser ist also
nicht mehr auf die Resonanzfrequenz des Atoms abgestimmt. Diese Asymmetrie in
der Streurate und im begleitenden Impulsübertrag der Atome, die sich nach links
bzw. nach rechts bewegen, führt zum gewünschten Kühleffekt. Wird ein Atom drei
wechselseitig orthogonalen, einander schneidenden Paaren von gegenläufigen
Laserstrahlen ausgesetzt, die auf nL < n0 abgestimmt sind, dann erfährt das Atom eine dämpfende bzw.
kühlende Wirkung, unabhängig von seiner Bewegunsgrichtung. Solch eine
Konfiguration wird als "optische Melasse" bezeichnet.
/c) < nL < n0 ist; der Laser ist also
nicht mehr auf die Resonanzfrequenz des Atoms abgestimmt. Diese Asymmetrie in
der Streurate und im begleitenden Impulsübertrag der Atome, die sich nach links
bzw. nach rechts bewegen, führt zum gewünschten Kühleffekt. Wird ein Atom drei
wechselseitig orthogonalen, einander schneidenden Paaren von gegenläufigen
Laserstrahlen ausgesetzt, die auf nL < n0 abgestimmt sind, dann erfährt das Atom eine dämpfende bzw.
kühlende Wirkung, unabhängig von seiner Bewegunsgrichtung. Solch eine
Konfiguration wird als "optische Melasse" bezeichnet.
Die Zufälligkeiten der Absorptionszeitpunkte und der Richtung der Reemission der Photonen wirken wie ungeordnete Stösse auf das Atom, die dem Kühleffekt entgegenwirken. Diese ungeordneten Stösse, die eine Aufheizung hervorrufen, sind dann mit der Kühlwirkung im Gleichgewicht, wenn die effektive Temperatur der Atome einen Minimalwert erreicht, der gleich h n / (2 kB) ist (darin ist kB die Boltzmann-Konstante). Bei den meisten Atomen liegt dieser Temperaturgrenzwert der Doppler-Kühlung bei 1 mK.
Mit Ionenfallen erreicht man normalerweise eine starke Einschlusswirkung, während neutrale Atome relativ schwach gehalten werden. Atome mit kinetischen Energien grösser als etwa 1 K können aus den meisten Neutralatom-Fallen entweichen. Daher müssen Neutralatom-Fallen durch eine zusätzliche Kühlung ergänzt werden, wenn sie mit anfänglich heissen Atomen (bei Zimmertemperatur) beschickt werden. Die magnetooptische Atomfalle (MOT, vom engl. Ausdruck magneto-optical trap) für neutrale Atome bewirkt sowohl Einschluss als auch Kühlung der Atome. Die MOT ist eine in der Atomphysik inzwischen häufig eingesetzte Quelle kalter und dichter atomarer Proben.
Sie nutzt denselben Effekt, der auch Grundlage der oben beschriebenen Laserkühlung ist. Jedoch läuft der Absorptions- und Reemissions-Prozess, der Impuls von Photonen auf Atome übertragen kann, oft mittels Übergängen zwischen zwei oder mehreren Elektronenniveaus im Atom ab. Nach dem Zeeman-Effekt hängt die Energie eines bestimmten Niveaus von der Orientierung des Bahndrehimpulses relativ zu einem angelegten Magnetfeld ab. Die MOT nutzt diese Abhängigkeit vom Magnetfeld aus, um die Photonenstreuung zu steuern und die Atome zu einem bestimmten Punkt im Raum zu bewegen.
Für die nähere
Erklärung der MOT nehmen wir an, dass der energetisch niedrigere
Elektronenzustand den Bahndrehimpuls null und damit auch ein magnetisches
Moment null aufweist; daher ist ein Elektron in diesem Zustand nicht sensitiv
für Magnetfelder. Weiterhin soll der angeregte Elektronenzustand einen
Bahndrehimpuls mit der Quantenzahl eins haben; in diesem Fall spaltet der
angeregte Zustand in drei einzelne Zustände auf, die den drei möglichen
Orientierungen des Bahndrehimpulses des angeregten Zustands relativ zu einem
äusseren Magnetfeld entsprechen (parallel, im rechten Winkel und antiparallel);
die z-Komponente des Drehimpulses dieser Zustände (also die Komponente
in Richtung des Magnetfelds) wird in Vielfachen von ![]() angegeben und beträgt + 1, 0 bzw. -1. Die
betreffenden Energien sind um einen Betrag gegen über dem feldfreien Zustand
verschoben, der proportional zur Magnetfeldstärke und zum Betrag des
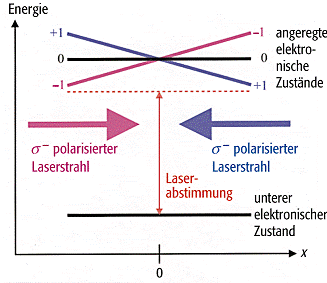
Bahndrehimpulses ist. In [33]Abb. 4 sind der Grundzustand und drei
angeregte elektronische Zustände eines Atoms dargestellt, und zwar als Funktion
der eindimensionalen Auslenkung x gegenüber einem angelegten
Magnetfeldgradienten, wobei bei x = 0 die Feldstärke null ist.
angegeben und beträgt + 1, 0 bzw. -1. Die
betreffenden Energien sind um einen Betrag gegen über dem feldfreien Zustand
verschoben, der proportional zur Magnetfeldstärke und zum Betrag des
Bahndrehimpulses ist. In [33]Abb. 4 sind der Grundzustand und drei
angeregte elektronische Zustände eines Atoms dargestellt, und zwar als Funktion
der eindimensionalen Auslenkung x gegenüber einem angelegten
Magnetfeldgradienten, wobei bei x = 0 die Feldstärke null ist.
Wenn ein Laserstrahl
entlang der x-Achse s + -zirkular polarisiert ist - jedes Photon hat dann einen
Drehimpuls mit der Quantenzahl + 1 -, so wird wegen der Drehimpulserhaltung bei
Absorption eines Photons aus diesem Strahl das Atom in einen Zustand mit der
Quantenzahl + 1 angehoben; entsprechend wird ein s - -polarisierter Strahl
das Atom in einen angeregten Zustand mit der Quantenzahl -1 bringen. In einer
Dimension betrachtet, treten in die MOT ein s + -Strahl von rechts und
ein s
- -Strahl von links ein;
der Magnetfeldgradient entspricht der Darstellung in [34]Abb. 4. Wenn beide Laserstrahlen so
abgestimmt sind, dass ihre Frequenzen etwas unterhalb der Resonanzfrequenz
liegen, so bestimmt die Zeeman-Verschiebung der angeregten Zustände, aus
welchem Strahl das Atom bevorzugt Photonen streut. Ein Atom rechts vom Zentrum
(x > 0)
streut mehr s
+ -Photonen, die von rechts ankommen; entsprechend streut ein Atom
links vom Zentrum (x < 0) mehr s - -Photonen, die von links ankommen. Das führt zu einer
resultierenden Kraft, die die Atome unabhängig von ihrer genauen Position zum
Zentrum (x = 0) hin stossen. Weil die Frequenzen der Laserstrahlen
ausserdem unterhalb der Resonanzfrequenz aller möglicher Übergänge nahe der
Fallenmitte liegen, tritt zudem auch eine laserkühlende Wirkung der oben
beschriebenen Art auf.
Dieser Einschluss und die
Kühlwirkung können leicht auf die drei Dimensionen ausgedehnt werden, indem
ähnlich wie bei der oben erwähnten Konfiguration der "optischen
Melasse" sechs Laserstrahlen auf die Fallenmitte gerichtet werden. Eine
typische magnetooptische Falle (MOT) kann bis zu 109 Atome in einem Volumen von einigen mm3 einschliessen, wobei die
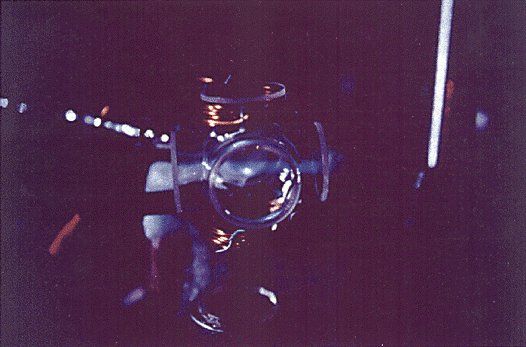
Temperatur unter 1 mK liegt. [35]Abb. 5 zeigt eine MOT, die rund 107
Caesiumatome enthält.
Die MOT-Technik erlaubt die Akkumulation von Atomen für eine Vielzahl von Anwendungen, beispielsweise für moderne Atomuhren, für lithographische Anordnungen von Atomen auf Oberflächen sowie für verschiedene Untersuchungen von Wechselwirkungen zwischen Atomen und Licht und von Atomstössen. Die MOT ist ein wichtiges Hilfsmittel zur Erzeugung eines Bose-Einstein-Kondensats eines atomaren Gases. Sie erwies sich auch in anderen Bereichen als nützlich, so bei der Anreicherung seltener (teilweise radioaktiver) Isotope, die mit Hilfe konventioneller Atomquellen nur schwierig zu untersuchen sind.
Der Einfang und die Laserkühlung geladener oder neutraler Atome in elektromagnetischen Fallen eröffnete neue Möglichkeiten für präzise atomphysikalische Experimente, die von der Behandlung und der exakten Kontrolle einzelner Atome bis zur Untersuchung kollektiver Effekte von Millionen von Atomen bei hoher Dichte und tiefen Temperaturen reichen.
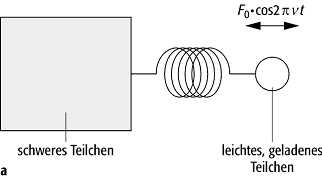
Atom- und Ionenfallen 1: Fallen, die die ponderomotorischen Kräfte ausnutzen: a) Schematische Darstellung eines (leichten) geladenen Teilchens, das über eine Feder mit einem schwereren Teilchen verbunden ist, beispielsweise ein Elektron mit einem Atomkern. Die Frequenz der Schwingung zwischen den Teilchen ist mit n0 bezeichnet. Wenn die angelegte Kraft (F0 cos 2pnt) räumlich inhomogen ist, wirkt die resultierende mittlere ponderomotorische Kraft zum Gebiet der geringeren (bzw. der höheren) Feldstärke hin, wenn n > n0 (bzw. < n0) ist. Wenn auf das Atom ein Laserfeld mit einer Frequenz nahe einem optischen Übergang (rund 5 × 1014 Hz) wirkt, so kann der frequenz- und richtungsabhängige Verlauf der Intensität so eingestellt werden, dass eine optische Dipolkraft auftritt, die das Elektron (und damit das Atom) in der Falle festhält. Bei n0 = 0 sind schweres und leichtes Teilchen unabhängig voneinander. In diesem Fall gilt immer n > n0 = 0, und das geladene Teilchen - beispielsweise ein atomares Ion - wird im Gebiet geringster Feldintensität eingefangen (die Bewegung des schweren Teilchens kann hier vernachlässigt werden). b) Elektrodenanordnung einer Paul-Falle oder Radiofrequenz-Ionenfalle. Zwei "Deckelelektroden" sind beiderseits einer Ringelektrode angebracht; zur besseren Übersicht ist letztere angeschnitten gezeichnet. Die elektrische Feldstärke weist im Zentrum zwischen den Elektroden den Wert null (bzw. ein Minimum) auf; hier werden die Ionen festgehalten.
Atom- und Ionenfallen 2: Atomuhren mit einem Atom. Links sind die Elektroden einer Paul- oder Radiofrequenz-Falle zum Grössenvergleich auf einer Münze dargestellt. Das rechte Bild zeigt die Photographie eines einzelnen, lasergekühlten Quecksilberions (der helle Punkt, auf den der Pfeil weist), das sich im Zentrum dieser Falle befindet. Weil ultraviolettes Licht unsichtbar ist, wurde das Bild mit einer Videokamera aufgenommen, die auch UV-empfindlich ist. Ein einzelnes atomares Ion in einer Falle ist sehr unempfindlich gegenüber Einflüssen aus der näheren Umgebung und kann daher für eine extrem genaue Atomuhr genutzt werden.
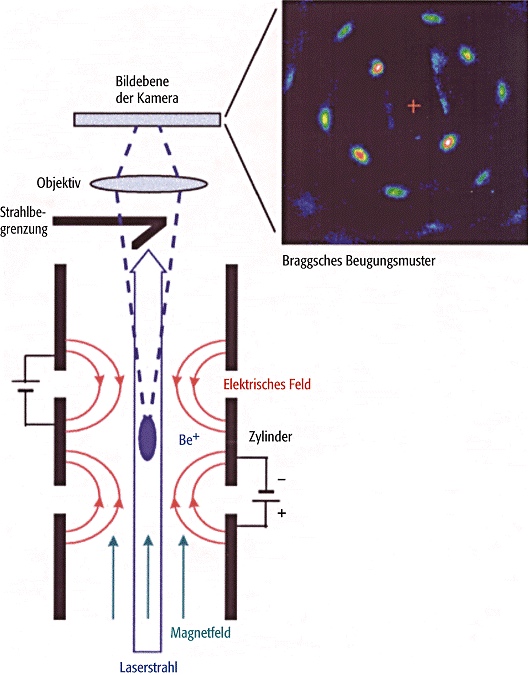
Atom- und Ionenfallen 3: Kristalline Plasmen. Hier ist ein lasergekühltes Berylliumionen-Plasma schematisch dargestellt (dunkles Sphäroid); es wird durch eine Kombination statischer elektrischer und magnetischer Felder eingeschlossen (Penning-Ionenfalle). Bei tiefen Temperaturen kondensieren die Ionen zu einem kubisch raumzentrierten (bcc) Kristallgitter, so dass sich ein entsprechendes Bragg-Beugungsmuster ergibt. Dieses Muster muss stroboskopisch erfasst werden, weil das Plasma um die Achse der einschliessenden Felder rotiert.
Atom- und Ionenfallen 4: Magnetooptische Falle (MOT). Hier sind - in einer Raumrichtung - die atomaren Energieniveaus in einer MOT schematisch dargestellt. Im unteren elektronischen Zustand ist der Bahndrehimpuls l = 0, und im angeregten Zustand gilt ohne äusseres Magnetfeld l = 1. Ein magnetisches Gradientenfeld wird angelegt, wobei bei x = 0 die Feldstärke null ist. Dies führt zu einer Aufspaltung in drei angeregte Energieniveaus mit den Bahndrehimpulsquantenzahlen - 1, 0 und + 1. Laserstrahlen, die von rechts bzw. von links kommen, werden auf eine etwas niedrigere Frequenz als die der Resonanz abgestimmt; sie sind positiv bzw. negativ zirkular polarisiert, so dass sie ausschliesslich mit dem angeregten Zustand + 1 bzw. - 1 wechselwirken. Ein Atom bei x > 0 (bzw. bei x < 0) streut mehr Photonen in dem von rechts (bzw. von links) ankommenden Laserstrahl. Dadurch ergibt sich eine Fallenkraft, die das Atom ungeachtet seiner momentanen Position zum Zentrum (x = 0) hin drückt.
bottom:.0001pt;border:none; mso-border-left-alt:solid purple 1.5pt;mso-border-bottom-alt:solid purple 1.5pt; mso-border-right-alt:solid purple 1.5pt;padding:0cm;mso-padding-alt:0cm 13.0pt 13.0pt 13.0pt\'>Atom- und Ionenfallen 5: Caesiumatome in einer magnetooptischen Falle. Die helle Lichtkugel in der Bildmitte ist eine Ansammlung von rund 107 Caesiumatomen mit einem Durchmesser von einigen Millimetern. Die Spulen, die den Magnetfeldgradienten erzeugen, sind darüber und darunter zu erkennen; sie sind um eine evakuierte Glaszelle gewickelt. Die (nicht sichtbaren) Laserstrahlen treten aus sechs Richtungen ein und sind auf die Atome gerichtet.
Techniklexikon.net
Das freie Technik-Lexikon. Fundierte Informationen zu allen Fachgebieten der Ingenieurwissenschaften, für Wissenschaftler, Studenten, Praktiker & alle Interessierten. Professionell dargeboten und kostenlos zugängig.
Techniklexikon
Modernes Studium der Physik sollte allen zugängig gemacht werden.