Techniklexikon

Trigonometrie

Mathematische Methoden und Computereinsatz, die mathematische Disziplin, die sich mit den Beziehungen von Winkeln und Seiten in ebenen und sphärischen Dreiecken beschäftigt. Der Hauptgegenstand der Trigonometrie sind die Winkelfunktionen (Kreisfunktionen) Cosecans, Cosinus, Secans, Sinus, Tangens und Cotangens, die ihre elementare Definition im rechtwinkligen Dreieck für Winkel zwischen 0°und 90° erfahren und dann im Einheitskreis schliesslich für beliebige Winkel definiert werden. Seien die Hypotenuse eines rechtwinkligen Dreiecks mit  und die beiden Katheten mit  und  bezeichnet; letzteren gegenüber mögen die Winkel  und  liegen (siehe Abb. 1). Die elementaren Definitionen im rechtwinkligen Dreieck lauten dann:

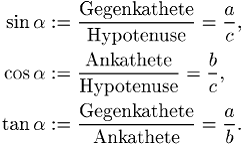
Die übrigen Winkelfunktionen ergeben sich zu

Aus der entsprechenden Verallgemeinerung, bei der das rechtwinklige Dreieck in einem Einheitskreis plaziert wird (siehe Abb. 2), folgen die Vorzeichen für ,  und  in den einzelnen Quadranten,

sowie der Beweis, dass die Winkelfunktionen 2p-periodische,  und  sogar p-periodische Funktionen sind; es gilt  und  sowie  und . Desweiteren folgen aus der Definition von  und  im rechtwinkligen Dreieck und den Vorzeichen im Einheitskreis die Wertebereiche  und . Für spezielle Winkel lassen sich die Werte der Winkelfunktionen aus der Tabelle ablesen. Algebraisch lassen sich  und  auch mit Hilfe der komplexen Exponentialfunktionen in der Form

definieren. Damit, oder auch elementargeometrisch, lassen sich eine Vielzahl nützlicher Beziehungen und Additionstheoreme zwischen den Winkelfunktionen beweisen (siehe Nachsatz Band 3).

Im allgemeinen ebenen Dreieck sind der Sinussatz

und der Cosinussatz

von Bedeutung. Die Trigonometrie spielt eine wichtige Rolle in vielen geometrischen, auf Dreiecksberechnungen basierenden Problemen, z.B. in der Landvermessung. In Physik und Technik treten die Winkelfunktionen häufig im Zusammenhang mit der elementaren Vektorrechnung auf. In der Astronomie wird insbesondere die sphärische Trigonometrie –hier gelten entsprechende Varianten von Cosinussatz und Sinussatz im Kugeldreieck – gebraucht.

Trigonometrie: Spezielle Werte der trigonometrischen Funktionen.

bottom:solid gray 1.0pt;border-right: none;mso-border-top-alt:solid gray .75pt;mso-border-left-alt:solid black .75pt; mso-border-bottom-alt:solid gray .75pt;padding:0cm 3.5pt 0cm 3.5pt\'>	bottom:solid gray 1.0pt;border-right:none;mso-border-top-alt: solid gray .75pt;mso-border-bottom-alt:solid gray .75pt;padding:0cm 3.5pt 0cm 3.5pt\'> sin	bottom:solid gray 1.0pt;border-right:none;mso-border-top-alt: solid gray .75pt;mso-border-bottom-alt:solid gray .75pt;padding:0cm 3.5pt 0cm 3.5pt\'> cos	bottom:solid gray 1.0pt;border-right:solid black 1.0pt; mso-border-top-alt:solid gray .75pt;mso-border-bottom-alt:solid gray .75pt; mso-border-right-alt:solid black .75pt;padding:0cm 3.5pt 0cm 3.5pt\'> tan
0°	0	1	0
30°
45°			1
60°
bottom:solid gray 1.0pt;border-right:none; mso-border-left-alt:solid black .75pt;mso-border-bottom-alt:solid gray .75pt; padding:0cm 3.5pt 0cm 3.5pt\'> 90°	bottom:solid gray 1.0pt; mso-border-bottom-alt:solid gray .75pt;padding:0cm 3.5pt 0cm 3.5pt\'> 1	bottom:solid gray 1.0pt; mso-border-bottom-alt:solid gray .75pt;padding:0cm 3.5pt 0cm 3.5pt\'> 0	bottom:solid gray 1.0pt;border-right:solid black 1.0pt; mso-border-bottom-alt:solid gray .75pt;mso-border-right-alt:solid black .75pt; padding:0cm 3.5pt 0cm 3.5pt\'>

 

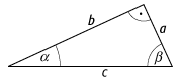
Trigonometrie 1: Seiten und Winkel im rechtwinkligen Dreieck.

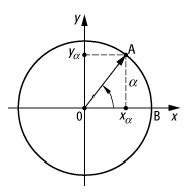
Trigonometrie 2: Konstruktion der Winkelfunktionen am Einheitskreis.

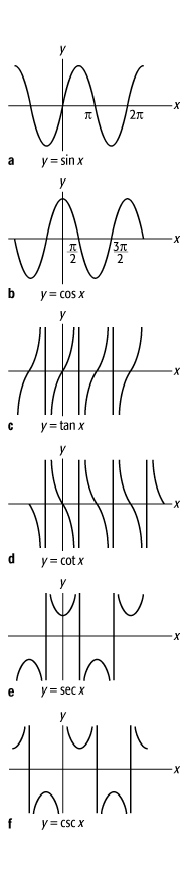
Trigonometrie 3: Graphen der Winkelfunktionen. a) Sinus, b) Cosinus, c) Tangens, d) Cotangens, e) Secans, f) Cosecans.