Techniklexikon

Neuronale Netze

Nichtlineare Dynamik, Chaos, Fraktale

Neuronale Netze sind dynamische Systeme, die aus einfach aufgebauten Einheiten, den Neuronen, bestehen, die über ein System von gerichteten Verbindungen miteinander wechselwirken. Sie wurden ursprünglich zur mehr oder weniger vereinfachten und idealisierten Modellierung biologischer Neuronenverbände entwickelt. Man spricht deshalb zur Unterscheidung von den natürlichen Systemen auch von künstlichen neuronalen Netzen, englisch Artificial Neural Networks.

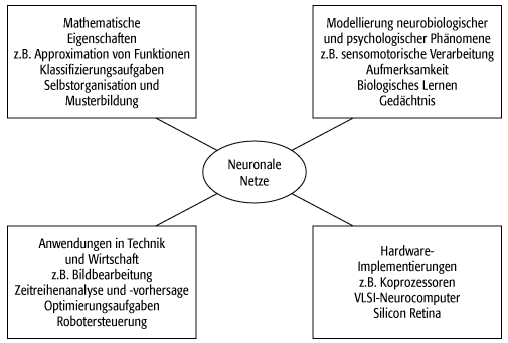
Seit dem Erscheinen des Artikels »A logical calculus of the ideas immanent in nervous activity« von Warren McCulloch und Walter Pitts im Jahr 1943 hat sich das Gebiet der neuronalen Netze in verschiedene Richtungen entwickelt, die z.T. gänzlich ausserhalb der ursprünglich intendierten neurobiologischen Anwendungsfelder liegen (siehe [41]Abb. 1). Einer dieser Zweige beschäftigt sich mit den mathematischen Aspekten; als Themen seien die Approximation von Funktionen durch neuronale Netze und zeitliche und räumliche Selbstorganisation (Synchronisation neuronaler Aktivität, Musterbildung in räumlich strukturierten Netzen) genannt. Ein zweites Forschungsgebiet verwendet neuronale Netze zur Modellierung neurobiologischer, psychologischer und linguistischer Phänomene. Zu diesen gehören beispielsweise Eigenschaften sensorischer und motorischer Verarbeitung (visuelles Auflösungsvermögen, Koordination von Bewegungen usw.), aber auch kognitive Leistungen wie Aufmerksamkeit und Gedächtnis. Die Flexibilität neuronaler Netzwerke durch die Anpassung der Synapsenstärken hat zum dritten zu Anwendungen in Technik und Wirtschaft geführt; Beispiele hierfür sind die Wiedererkennung verrauschter Muster in der Bildverarbeitung, die Vorhersage von Zeitreihen und die Steuerung autonomer Roboter. Obwohl neuronale Netze zumeist auf herkömmlichen Computern implementiert werden, ist in den letzten Jahren zum vierten spezielle auf Parallelverarbeitung basierende Hardware entwickelt worden, die eine schnelle Simulation auch grosser Netze ermöglicht.

Die Neuronen künstlicher neuronaler Netze besitzen wesentliche Eigenschaften biologischer Nervenzellen, und ihre Wechselwirkung orientiert sich an der elektrischen und chemischen Signalübertragung im Gehirn. Man unterscheidet zwei Arten der Dynamik, die auf unterschiedlichen Zeitskalen ablaufen: schnelle neuronale Vorgänge (Aufnahme, Verarbeitung und Weitergabe von Signalen) auf der einen Seite und eine langsame Dynamik der Kopplungsstärken (Synapsenstärken) zwischen den Neuronen auf der anderen Seite. Durch die Veränderung der Kopplungsstärken kann das Verhalten des Netzwerks interaktiv oder selbstorganisiert verändert und an gewünschte Aufgaben angepasst werden; man spricht in diesem Fall von Lernen. Neuronale Netze unterscheiden sich hinsichtlich des verwendeten Neuronenmodells, der Netzwerkarchitektur und der Natur der Lernregel zur Veränderung der Synapsenstärken.

Nach einem kurzen Überblick über neurobiologische Grundlagen werden im folgenden einige Standardmodelle, ihre mathematischen Eigenschaften und Anwendungen vorgestellt.

 

1 Neurobiologische Grundlagen

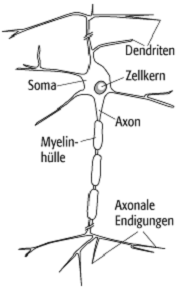
Biologische Neuronen dienen der Aufnahme, Verarbeitung und Weiterleitung von Signalen (siehe [42]Abb. 2). Diese Signale haben die Form raumzeitlicher Spannungsänderungen (Potentialänderungen) über der Zellmembran. Im Ruhezustand ist das Zellinnere negativ gegenüber dem Aussenraum und die Spannung beträgt ca. -70 mV (Ruhepotential).

Die Dendriten stellen die Eingangsfasern des Neurons dar. Sie sind besetzt mit bis zu 10⁵ Kontaktstellen, den Synapsen, über die das Neuron Signale von anderen Nenrvenzellen empfängt. Die Signale breiten sich im Dendritenbaum und bis zum Zellkörper (Soma) aus. Überschreitet durch Depolarisation der Membran die Spannung am Soma einen Schwellenwert von ca. -40 mV, so wird am Ansatzpunkt der Nervenfaser (Axon) eine pulsförmige solitäre elektrische Welle (Aktionspotential, Spike) ausgelöst, die entlang der Nervenfaser zu den axonalen Endigungen läuft: das Neuron feuert. Zur Erhöhung der Signalgeschwindigkeit sind manche Axone von einer isolierenden Proteinschicht, der Myelinhülle (Myelinscheide), umgeben. An den axonalen Endigungen schliesslich wird das elektrische Signal über Synapsen an nachgeschaltete Neuronen oder Muskelfasern übertragen.

Die synaptische Signalübertragung erfolgt entweder durch direkte elektrische Kopplung oder auf chemischem Wege. Bei der chemischen Synapse bewirkt ein ankommendes Aktionspotential in der vorgeschalteten Zelle die Ausschüttung von Transmitterstoffen, die zur nachgeschalteten Zelle diffundieren und dort aufgenommen werden. Als Folge davon kommt es in der nachgeschalteten Zelle zu einer Änderung der Membranspannung, zu einem postsynaptischen Potential. Chemische Synapsen können erregend (exzitatorisch) oder hemmend (inhibitorisch) wirken, je nach Vorzeichen des postsynaptischen Potentials.

Wird eine Nervenzelle erregt, so antwortet sie i.a. mit einer Serie von Aktionspotentialen, einem Spiketrain; [43]Abb. 3 zeigt ein Beispiel. Der Abstand zweier Spikes kann dabei nicht beliebig klein sein, da die Zelle nach der Erzeugung eines Spikes für eine kurze Zeit, der Refraktärzeit, in eine Regenerationsphase geht.

 

2 Neuronenmodelle

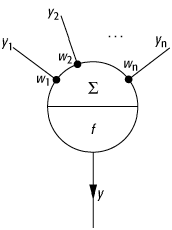
Für das Studium neuronaler Netze wird unterschiedlich stark von den komplexen Eigenschaften biologischer Neuronen abstrahiert. In Netzen mit diskreter Zeitstruktur verwendet man das in [44]Abb. 4 dargestellte, stark vereinfachte Neuronenmodell. Das Neuron bekommt Eingaben , die entweder von anderen Neuronen stammen oder äussere Eingaben in das Netzwerk darstellen. Die Eingaben werden durch Multiplikation mit den Synapsenstärken  gewichtet. Die Aktivierung h des Neurons beträgt

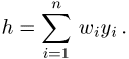
Für  wirkt die Eingabe  exzitatorisch, für  inhibitorisch (). Die Ausgabe  des Neurons wird durch Anwendung einer Ausgabefunktion  berechnet: .

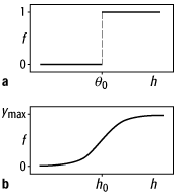
Im einfachsten Fall, dem sog. McCulloch-Pitts-Neuron, sind die Eingaben und die Ausgabe binär () und werden als »Feuern« bzw. »Nicht-Feuern« interpretiert. Für McCulloch-Pitts-Neuronen stellt  die Heaviside-Funktion  dar,

wobei  der Schwellenwert für das Feuern des Neurons ist ([45]Abb. 5a).

Nehmen die  kontinuierliche Werte an, spricht man von einem Analogneuron, und die Ausgabe  wird als mittlere Anzahl von Spikes interpretiert, die das Neuron pro Zeiteinheit erzeugt (Feuerrate). Für Analogneuronen verwendet man eine sigmoide Ausgabefunktion, d.h. eine stetige und monotone Funktion, die von Null auf einen Maximalwert  ansteigt. Als Beispiel sei die Fermi-Funktion

genannt, wobei  die Aktivierung angibt, bei der das Neuron mit der Rate  feuert (Abb. 5b).

Neben den bisherigen deterministischen Modellen kann man auch Neuronen mit stochastischer Ausgabefunktion betrachten. Bei gegebener Aktivierung h wird dabei die Wahrscheinlichkeit berechnet, mit der ein binäres Neuron die Ausgabe  erzeugt.

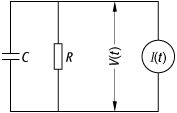
Das gebräuchlichste Neuronenmodell für Netzwerke mit zeitkontinuierlicher Dynamik ist das Integrate-and-Fire-Neuron. Die dynamische Variable ist das Membranpotential , wobei das Ruhepotential zumeist auf Null gesetzt wird. [46]Abb. 6 zeigt das unterhalb der Feuerschwelle  gültige Ersatzschaltbild. R ist der Widerstand und C die Kapazität der Zellmembran; die Stromquelle  modelliert die Eingabe des Neurons auf Grund der Spikeaktivitäten der anderen Neuronen im Netzwerk. Für  gilt die lineare Gleichung

mit einer Anfangsbedingung . Erreicht das Membranpotential zu einer Zeit  die Feuerschwelle, , so gibt das Neuron einen Spike ab und das Membranpotential wird auf Null gesetzt: . Refraktärzeiten können durch eine zeitabhängige Feuerschwelle, , berücksichtigt werden. Für die auftretenden Ströme  wählt man gemäss dem Pulscharakter der Spikes die Delta-Funktion, oder man berücksichtigt postsynaptische Potentiale in Form einer Alpha-Funktion:

mit  für Exzitation und  für Inhibition.

Neben den beschriebenen gibt es weitere, insbesondere komplexere Neuronenmodelle, die die räumliche Struktur des in [47]Abb. 2 dargestellten Neurons berücksichtigen. Zur Simulation grösserer Netzwerke verwendet man wegen des geringeren Rechenaufwandes jedoch zumeist einfachere Modelle.

 

3 Das Hopfield-Modell

John Hopfield schlug 1982 ein neuronales Netz vor, das einen Assoziativspeicher darstellt: Dem Netz können durch Wahl der Synapsenstärken Muster eingeprägt werden, und bei späterer Präsentation eines verrauschten oder unvollständigen Musters ist es in der Lage, das ursprüngliche Muster zu reproduzieren. Hopfield-Netze werden deshalb in der Bildverarbeitung eingesetzt. Das Hopfield-Modell hat ausserdem Bedeutung erlangt auf Grund seiner exakten Lösbarkeit und seiner formalen Analogie zum Ising-Modell in der Physik der Spingläser.

Das Netz besteht aus N McCulloch-Pitts-Neuronen, wobei als Ausgabewerte anstatt 0 und 1 üblicherweise -1 (nicht aktiv) und 1 (aktiv) gewählt werden. Alle Neuronen sind miteinander verbunden. Bekommt Neuron i () die Eingaben  (), so berechnet sich seine Ausgabe zur Zeit t + 1 gemäss

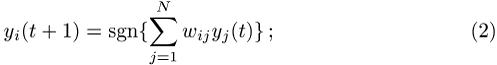
dabei ist  die Signum-Funktion ( für ,  für ), und  stellt die Synapsenstärke dar, mit der Neuron j auf Neuron i projiziert. Die Dynamik des Netzes ist asynchron, d.h. in jedem Zeitschritt erfolgt die zufällige Auswahl eines Neurons i und die Berechnung seiner Aktivität .

Für Netze mit symmetrischen Kopplungen, , existiert eine Energiefunktion

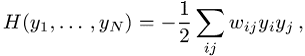
die unter der Dynamik (2) monoton fallend ist. Damit läuft das Netzwerk für beliebige Anfangsbedingungen in eines der lokalen Minima der Energiefunktion; ein so erreichter Zustand  ist stabil. Wählt man eine graphische Darstellung durch Farbkodierung (Aktivität 1 schwarz, Aktivität -1 weiss ) und eine rechteckige Anordnung der Neuronen, so entspricht jedem Minimum ein stabiles Muster, das bei Wahl der Anfangsbedingungen in seinem Einzugsbereich angelaufen wird ([48]Abb. 7).

Durch geeignete Wahl der Synapsenstärken  ist es möglich, vom Benutzer gewünschte Muster im Netzwerk zu speichern. Sei das m-te Muster gegeben durch  mit  (); dann existieren für

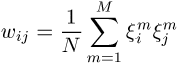
an den entsprechenden Stellen Minima der Energiefunktion.

In einem Hopfield-Netz lassen sich nicht beliebig viele Muster speichern. Rechnungen zeigen, dass im Mittel bei  ein Phasenübergang stattfindet, jenseits dessen keine Stabilität der Muster mehr erwartet werden kann. Die besten Speichereigenschaften hat das Hopfield-Netz für voneinander unabhängige Zufallsmuster, was bei realen Bildern im allgemeinen nicht der Fall ist.

 

4 Der Backpropagation-Algorithmus

Während bei Hopfield-Netzen die Synapsenstärken vorgegeben werden, stellt der Backpropagation-Algorithmus ein überwachtes Lernverfahren dar: dem Netz werden M Eingabemuster präsentiert, die jeweils mit einem Ausgabemuster assoziiert werden sollen. Der Fehler, den das Netzwerk dabei macht, wird durch Änderung der Synapsenstärken gemäss einem Gradientenverfahren minimiert. Backpropagation-Netze haben zahlreiche Anwendungen gefunden. Am bekanntesten ist wohl das von Terrence J. Sejnowski und Charles R. Rosenberg entwickelte NETtalk, dessen Eingabe aus englischem Text besteht. Der Text wird durch das Netzwerk in Ketten von Phonemen umgewandelt, die von einem Sprachsynthesizer wiedergegeben werden können.

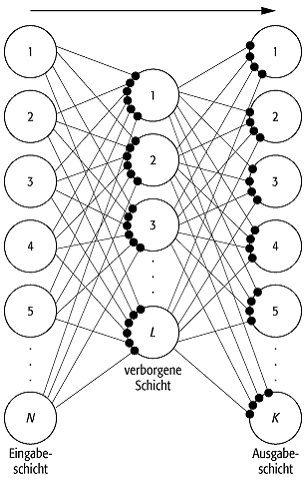
Backpropagation-Netze (auch Multilayer-Perceptrons genannt) bestehen aus Schichten von Analogneuronen, wobei jede Schicht mit zufällig initialisierten Kopplungsstärken vollständig an die nachfolgende gekoppelt ist, jedoch keine Verbindungen zu vorherigen Schichten oder zwischen den Neuronen einer Schicht bestehen ([49]Abb. 8). Es handelt sich um sog. vorwärtsgerichtete Netze, im Gegensatz zu rückgekoppelten Netzen wie beispielsweise den Hopfield-Netzen. An die Eingabeschicht werden nacheinander M Eingabemuster in Form von N-dimensionalen reellen Vektoren  angelegt. Die Eingabeneuronen haben keine Dynamik, sondern leiten ihre Eingaben ohne Änderung weiter. Die Aktivität wird wie in Abschnitt 3 beschrieben über die verborgenen Schichten bis zu den K Neuronen der Ausgabeschicht propagiert, die die Ausgaben  erzeugen. Die gewünschten Ausgabemuster seien  (jeweils ). Nach Präsentation aller Muster wird der Fehler des Netzwerks in Form der Summe aller quadratischen Abweichungen zwischen  und  berechnet:

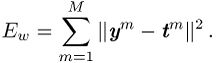
 ist eine Funktion sämtlicher Synapsenstärken im Netzwerk, symbolisiert durch den Index w.

Die Lernregel, d.h die Änderung der Synapsenstärken jeweils nach Präsentation der M Muster, hat die Form eines Gradientenabstiegs. Mit  ist

wobei  als Lernrate bezeichnet wird und  die Stärke einer beliebigen Synapse zwischen Neuron j und Neuron i im Netzwerk darstellt.

Im folgenden sei die Ausgabefunktion die Fermi-Funktion (1) mit , für die die Funktionalgleichung  gilt. Dann lässt sich für die rechte Seite von (3) folgende Rechenvorschrift angeben: Für jedes angelegte Muster  und jedes Ausgabeneuron k () wird für jeden Verbindungsweg  vom Ausgabeneuron zurück zur entsprechenden Synapse ein Produkt  von Faktoren berechnet, und es ist

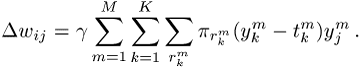
 ist die Ausgabe des Neurons i bei Präsentation des Musters m. Die Produkte  setzen sich wie folgt zusammen: i) Für jedes Neuron n entlang des Wegs ergibt sich ein Faktor , wobei  die Ausgabe dieses Neurons ist. ii) Für jede Synapse mit der Stärke  entlang des Wegs ergibt sich ein Faktor .

Als Beispiel diene das Netzwerk in [50]Abb. 8. Werden die Kopplungsstärken von der verborgenen Schicht zur Ausgabeschicht mit  und die von der Eingabeschicht zur verborgenen Schicht mit  bezeichnet, so gilt für :

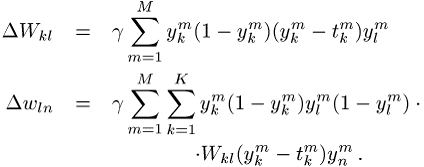
Zum beschriebenen Backpropagation-Algorithmus gibt es zahlreiche Erweiterungen, die insbesondere auf die Verbesserung der Konvergenzeigenschaften des Gradientenabstiegs und die Anwendbarkeit auf rekursive Netze zielen.

 

5 Kohonen-Netze

Teuvo Kohonen führte 1982 ein neuronales Netz ein, dessen Synapsenstärken sich organisieren, ohne dass eine Fehlerfunktion ausgewertet werden muss; das Kohonen-Netz verwendet ein unüberwachtes Lernverfahren. Die Eingaben in das Netz stammen aus einem metrischen Raum, beispielsweise einem Quadrat. Auch das Netzwerk hat eine räumliche Struktur: in vielen Fällen bilden die Neuronen eine lineare Kette oder ein zweidimensionales Gitter. Während des Lernvorgangs adaptieren die Synapsenstärken derart, dass die Neuronen den Eingaberaum nachbarschaftserhaltend repräsentieren. Eine Anwendung von Kohonen-Netzen besteht in der Modellierung von biologischen selbstorganisierenden Merkmalskarten, die sich beispielsweise in der menschlichen Grosshirnrinde finden: dort existieren Areale mit einer topographischen Repräsentation der visuellen Umwelt oder der Hautoberfläche.

Die Eingangssignale in das Netz sind Vektoren  eines k-dimensionalen Raums . Das Netzwerk  habe eine n-dimensionale Topologie, und jedes Neuron ist durch einen Ort  gekennzeichnet. Die Synapsenstärken zwischen dem Eingangssignal und dem Neuron  werden mit  bezeichnet. Für die neuronale Dynamik kann die Kopplung zwischen den Neuronen vernachlässigt werden. Somit berechnet sich im Falle von Analogneuronen deren Ausgabe als

wobei f die Fermi-Funktion (1) darstellt. Zu Beginn des Lernvorgangs werden die  zufällig initialisiert. Nach jeder Eingabe , die aus einer beliebigen Verteilung gezogen ist, wird dasjenige Neuron  bestimmt, dessen Aktivität maximal ist. Anstatt einer Berechnung der  nach (4) verwendet man dazu die einfache Bedingung

Die Lernregel besteht darin, dass für jedes Neuron  der Gewichtsvektor gemäss

verändert wird.  ist die Lernrate, und  ist eine Funktion, die basierend auf dem Abstand der Neuronen  und  in  die Stärke des Lernschritts bestimmt. Im allgemeinen wählt man für  eine Gausskurve, deren Breite im Verlauf des Lernvorgangs abnimmt, um das Netzwerk schliesslich »einzufrieren«. Anschaulich besagt (6), dass alle Gewichtsvektoren  in  in Richtung des Eingangssignals  gezogen werden, wobei die jeweilige Strecke sich aus der Metrik des Raums  der Neuronen bestimmt.

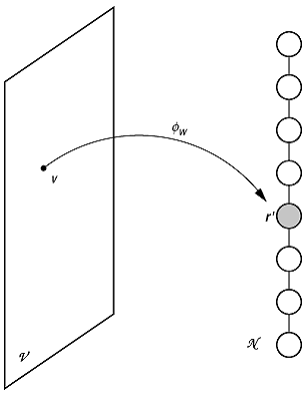
Gleichung (5) definiert eine von den Synapsenstärken abhängige Abbildung  von  in die Menge  der Neuronen (siehe [51]Abb. 9). Der Bildpunkt  ist gerade das Neuron mit der stärksten Antwort auf den Reiz v.  wird als neuronale Karte bezeichnet. Während des Lernvorgangs wird diese neuronale Karte verändert.

Für die Entwicklung der Synapsenstärken und die sich daraus ergebende Repräsentation des Eingangsraums  gibt es eine anschauliche Darstellung. Dabei werden für einen beliebigen Zeitpunkt die  in den Raum  eingezeichnet, und die Verbindung zwischen den Neuronen im Raum  wird durch Verbindungslinien zwischen den  symbolisiert. [52]Abb. 10 zeigt ein schematisches Beispiel für ein Quadrat  und eine Kette  von Neuronen. Die Synapsenstärken sind zufällig initialisiert (a). Die Eingangssignale liegen gleichverteilt in , und unter der Lerndynamik ordnen und entfalten sie sich (b-d), was zu einer nachbarschaftserhaltenden neuronalen Karte  führt. Auf Grund der möglichst guten Repräsentation des Quadrats durch die Neuronenkette bildet sich eine Kurve, die einer Iterierten einer Peano-Kurve entspricht.

Kohonen-Karten haben weitere interessante Eigenschaften. Liegen beispielsweise die Eingangssignale nicht gleichverteilt in , so ist in Gebieten mit höherer Signaldichte auch die Dichte der Synapsenstärken  grösser, so dass das Gebiet von überdurchschnittlich vielen Neuronen repräsentiert wird.

 

6 Synchronisation in Netzen aus spikenden Neuronen

Netzwerke mit zeitkontinuierlicher Dynamik werden häufig zur Modellierung neurobiologischer Systeme herangezogen. Die Wahl eines einfachen Neuronenmodells wie dem Integrate-and-Fire-Neuron erlaubt dabei teilweise einen analytischen Zugang. Ein aktuelles Forschungsgebiet ist die Untersuchung der Synchronisierung der Feueraktivitäten von Populationen gekoppelter Neuronen. Der Grund für das Interesse an diesem Gebiet liegt in der Vermutung, dass im Gehirn Synchronisation im Zusammenhang mit Gestaltwahrnehmung und verhaltensrelevanter Objekterkennung auftritt.

Renato E. Mirollo und Steven H. Strogatz studierten 1991 die Dynamik von Netzwerken vollständig exzitatorisch miteinander gekoppelter spikender Modellneuronen, die einen konstanten Eingabestrom bekommen. Sie zeigten, dass solche Netzwerke unter der neuronalen Dynamik für fast alle Anfangsbedingungen in einen Zustand evolvieren, in dem die Neuronen synchron mit der Phasenlage Null feuern. Erweiterungen dieser Untersuchung betreffen die Berücksichtigung von Signallaufzeiten zwischen den Neuronen, die in realen Systemen stets auftreten, und die Auswirkungen von Inhibiton und Exzitation. Das wesentliche Ergebnis ist, dass bei Vorhandensein von Zeitverzögerungen inhibitorische Kopplungen zur Bildung stabiler Cluster führen, deren Neuronen jeweils synchron feuern. Bei exzitatorischer Kopplung dagegen sind die sich ausbildenden Cluster nicht stabil, sondern zerfallen nach einigen Feuerperioden wieder und bilden sich spontan neu mit wechselnder neuronaler Zusammensetzung.

 

7 Ausblick

Das Gebiet der neuronalen Netze mit seiner etwas über 50-jährigen Geschichte zeigt sich nach wie vor unvollendet. Dies betrifft sowohl die mathematischen Eigenschaften selbst einfacher Netzwerke als auch die Anwendungen in Naturwissenschaft, Technik und Wirtschaft. Die Zahl der kommerziellen Anwendungen und der Beispiele, in denen neuronale Netze herkömmlichen Methoden überlegen sind, ist zur Zeit noch recht gering. Ein Grund für die Vorsicht, die man beispielsweise beim Einsatz neuronaler Netze für Steuerungsaufgaben walten lässt, liegt darin, dass die Netzwerkdynamik in vielen Fällen komplex und deshalb nicht durchschaubar ist. Der grosse Vorteil von neuronalen Netzen liegt aber in ihrer Flexibilität und ihrer Fähigkeit, sich ohne technische Fertigkeiten von seiten des Benutzers während des Gebrauchs an die jeweiligen Aufgaben anzupassen.

 

Literatur:

M. A. Arbib (Hrsg.): The Handbook of Brain Theory and Neural Networks, Cambridge, MA: MIT Press, 1995;

J. Hertz, A. Krogh, R.G. Palmer: Introduction to the Theory of Neural Computation, Redwood City, CA: Addison-Wesley, 1991;

W. Maass, C.M. Bishop (Hrsg.): Pulsed Neural Networks, Cambridge, MA: MIT Press, 1999;

H. Ritter, T. Martinetz, K. Schulten: Neuronale Netze, Bonn: Addison-Wesley, 1991;

R. Rojas: Theorie der neuronalen Netze, Berlin: Springer-Verlag, 1993;

A. Zell: Simulation neuronaler Netze, München: Oldenbourg, 1994.

 

neuronale Netze 1: Teildisziplinen.

neuronale Netze 2: Schematische Darstellung eines biologischen Neurons.

neuronale Netze 3: Spiketrain eines Mittelhirnneurons eines Salamanders als Antwort auf ein schwarzes bewegtes Rechteck, das dem Tier präsentiert wird. Die Aktionspotentiale sind als Striche dargestellt. Skala: 500 ms. (Daten mit freundlicher Genehmigung von B. Lienstädt.)

neuronale Netze 4: Modellneuron für Netze mit zeitdiskreter Dynamik. f ist das Symbol für die Ausgabefunktion.

neuronale Netze 5: Ausgabefunktionen für Modellneuronen. a) Um den Schwellenwert  verschobene Heaviside-Funktion für McCulloch-Pitts-Neuronen. b) Fermi-Funktion für Analogneuronen mit maximaler Feuerrate ; für  feuert das Neuron mit der Rate .

neuronale Netze 6: Ersatzschaltbild für das Integrate-and-Fire-Neuron unterhalb der Feuerschwelle.

neuronale Netze 7: Der Buchstabe »T« als Aktivitätsmuster eines Hopfield-Netzwerks. Entspricht der intakte Buchstabe (oben) einem Minimum der Energiefunktion, so wird er rekonstruiert, falls das Netzwerk mit einem verrauschten (Mitte) oder unvollständigen (unten) Muster gestartet wird.

neuronale Netze 8: Ein dreischichtiges Netzwerk mit  Eingabeneuronen,  verborgenen Neuronen und  Ausgabeneuronen. Schwarze Punkte symbolisieren Synapsen. Der Pfeil gibt die Richtung des Signalflusses an.

neuronale Netze 9: Eine neuronale Karte , die einen zweidimensionalen Eingangsraum auf eine eindimensionale Kette von Neuronen abbildet.

neuronale Netze 10: Abbildung zwischen einer Kette und einem Quadrat. a) zufällig gewählte Anfangszuordnung; b) Grobzuordnung nach 200 Markow-Schritten, c) nach 50 000 Markow-Schritten. d) Nach 100 000 Markow-Schritten ähnelt die erhaltene Zuordnung einer Peano-Kurve.