krummlinige Koordinaten

Karl-Wilhelm Steinfieber
jegliches System von
Koordinaten ![]() , in dem
mindestens eine der Koordinatenlinien ui
= const. keine Gerade, sondern eine gekrümmte Linie ist. Sei r = r(u) die Darstellung der kartesischen Koordinaten durch
die krummlinigen Koordinaten u. Der differentielle
Abstandsvektor ist in diesem System gegeben durch
, in dem
mindestens eine der Koordinatenlinien ui
= const. keine Gerade, sondern eine gekrümmte Linie ist. Sei r = r(u) die Darstellung der kartesischen Koordinaten durch
die krummlinigen Koordinaten u. Der differentielle
Abstandsvektor ist in diesem System gegeben durch
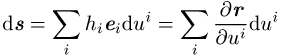
mit den Einheitsvektoren und Massstabs- oder Skalenfaktoren
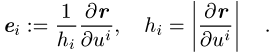
Daraus lässt sich das Linienelement
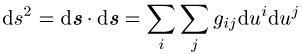
berechnen, wobei ![]() den kovarianten Metriktensor bezeichnet. Im
Falle eines diagonalen Metriktensors spricht man von orthogonalen Koordinaten;
den kovarianten Metriktensor bezeichnet. Im
Falle eines diagonalen Metriktensors spricht man von orthogonalen Koordinaten; ![]() ist dann allein durch die Massstabs- oder
Skalenfaktoren definiert:
ist dann allein durch die Massstabs- oder
Skalenfaktoren definiert: ![]() . In
krummlinigen Koordinaten genügt der Gradient
. In
krummlinigen Koordinaten genügt der Gradient ![]()
![]() der Darstellung
der Darstellung
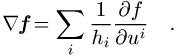
Techniklexikon.net
Das freie Technik-Lexikon. Fundierte Informationen zu allen Fachgebieten der Ingenieurwissenschaften, für Wissenschaftler, Studenten, Praktiker & alle Interessierten. Professionell dargeboten und kostenlos zugängig.
Techniklexikon
Modernes Studium der Physik sollte allen zugängig gemacht werden.