Techniklexikon

integrierender Faktor

Mathematische Methoden und Computereinsatz, Eulerscher Multiplikator, eine Funktion, mit deren Hilfe durch Multiplikation eine gewöhnliche Differentialgleichung integrabel bzw. exakt wird. Eine Differentialgleichung

heisst exakt, wenn es eine Stammfunktion F(x,y), d.h. eine Funktion mit stetigen partiellen Ableitungen  und , gibt und somit

gilt. Bei Kenntnis von F sind die Lösungen von (*) gerade gegeben durch die Funktionen , für die  konstant, d.h.  ist. Eine notwendige und hinreichende Bedingung für die Exaktheit von (*) ist . In der Praxis sind g und h gegeben, und ist  erfüllt, so bestimmt man zunächst eine Funktion  mit  und konstruiert dann  derart, dass auch  erfüllt ist.

Sei nun wieder die Differentialgleichung. (*) betrachtet, von der nun aber nicht gefordert wird, dass sie exakt ist. Eine Funktion

 heisst integrierender Faktor, wenn

exakt ist.

 ist integrierender Faktor genau dann, wenn

.

Beispiel: . Der integrierende Faktor für diese Differentialgleichung ist . Damit nimmt (**) nach Ausmultiplizieren und Umsortieren die Gestalt

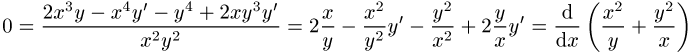
an, woraus als Lösung der Differentialgleichung die Kurvenschar

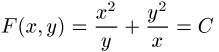 folgt.